Ejercicio obligatorio 1

Fecha de entrega: Domingo 3 de mayo

Introducción

Ondas

Una función de onda \(f(t)\) puede representarse en el tiempo \(t\) según la expresión:

\[f(t) = A\sin(2\pi f t + \phi),\]

donde \(A\) representa la amplitud, \(f\) la frecuencia angular (expresada en Hertz) y \(\phi\) la fase (expresada en radianes).

El estudio de las ondas tiene múltiples aplicaciones en la ingeniería dado que muchas variables físicas se propagan según este modelo.

Integración

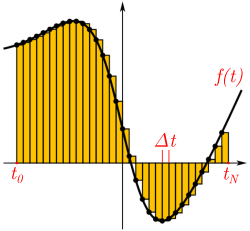
../_images/20201_ej1_int.png

Sabemos del CBC que la notación \(F(t) = \int_{t_0}^{t} f(t)\,dt\) representa a la integral de la función \(f(t)\) y esta función \(F(t)\) será el área acumulada de \(f(t)\) desde \(t_0\) hasta \(t\).

Sabemos que la integral de Reimann se define en términos de sumas sucesivas. Si sumáramos por la izquierda las áreas de \(N\) rectángulos nos quedaría:

\[\int_{t_0}^{t_N} f(t)\,dt = \lim_{\Delta t\to0} \sum_{i=0}^{N-1} f(t_i)\,\Delta t,\]

donde los \(t_i\) son una sucesión de \(N+1\) valores distribuidos uniformemente en el intervalo \([t_0, t_N]\) y \(\Delta t\) es tal que \(t_{i+1} = t_i + \Delta t\).

Si elimináramos el paso al límite, podemos obtener una aproximación discreta de la integral:

\[\int_{t_0}^{t_N} f(t)\,dt \approx \sum_{i=0}^{N-1} f(t_i)\,\Delta t.\]

Si fijamos \(\Delta t\) y llamamos \(F(t_N)\) a la expresión:

\[F(t_N) = \sum_{i=0}^{N-1} f(t_i)\,\Delta t,\]

podemos ver que con \(F(t_N)\) podemos aproximar a pasos discretos a la integral \(F(t)\) buscando un \(t_N = t\) o, lo que es lo mismo, esta aproximación se podrá evaluar en valores de \(t\) que coincidan con los \(t_i\) definidos antes.

Onda

Se pide implementar la función double onda(double t, float a, float f, float phi); que calcule la función de onda temporal en el instante t, donde a representa la amplitud, f la frecuencia angular y phi la fase.

Integral de la onda

Dadas las siguientes definiciones:

#define T0 0
#define TN 10
#define DELTAT 0.0005

#define A 50
#define F 29
#define PHI PI/2

Se pide implementar un programa que calcule la tabla de la integral F(t_i) entre los valores T0 \(\leq t \leq\) TN con intervalos de DELTAT donde la función f(t) es una onda de amplitud A, frecuencia F y fase PHI.

El programa deberá imprimir en formato CSV las columnas \(t_i\) y \(F(t_i)\) para cada uno de los valores.

Graficación

Se pide graficar los valores que genera el programa como salida en el software de su preferencia (planilla de cálculos, octave, gnuplot, etc.).

Realizar dos gráficos, uno con la serie completa y otro donde se vea un par de ciclos de la onda.

Validación

Se pide calcular por otro método el problema planteado (esto puede ser analíticamente, mediante otro software, etc.) y comparar la gráfica generada por este método con la gráfica generada por nuestro programa.

Entrega

Deberá entregarse:

  1. El código fuente del programa desarrollado.

  2. El gráfico de la integral con los valores extraidos de este programa.

  3. Una pequeña interpretación de las diferencias o similitudes entre los valores obtenidos y los valores esperados.

La entrega se realiza por correo a la dirección algoritmos9511entregas en gmail.com (reemplazar en por arroba).

El ejercicio es de entrega individual.