Ejercicio obligatorio 2
Fecha de entrega: Viernes 15 de mayo
Introducción
Sonido
La percepción que sentimos como sonido se debe a la vibración de ondas en el aire que es recibida e interpretada por nuestros oídos. En los sonidos podemos distinguir una intensidad, por la cual hay sonidos más fuertes que otros; un tono, por el cual hay sonidos más agudos y sonidos más graves; y un timbre, por el cual no todas las cosas que tienen el mismo tono suenan igual.
Sabemos que la expresión de una onda \(f(t)\) se representa en el tiempo \(t\) según la expresión:
En esta expresión \(a\) representa la intensidad y \(f\) representa la frecuencia del tono en Hertz. Esta onda es una onda pura.
Ahora bien en la naturaleza los sonidos nunca generan ondas puras, sino que un sonido de una determinada frecuencia fundamental \(f\) está siempre contaminado por armónicos que son múltiplos de dicha frecuencia. Es decir, un sonido real, para determinada intensidad \(a\) y determinado tono \(f\) tendrá una forma
donde \(F_i\) son las frecuencias relativas de los armónicos y \(A_i\) son las amplitudes relativas de ellos (observar que para una onda pura tenemos \(F = \{1\}\) y \(A = \{1\}\)).
Por ejemplo, para una frecuencia fundamental de 110 Hertz (lo que es un La de la segunda octava del piano) sumando la fundamental (en verde) y 7 armónicos más (en azul) obtenemos la onda final (en rojo):
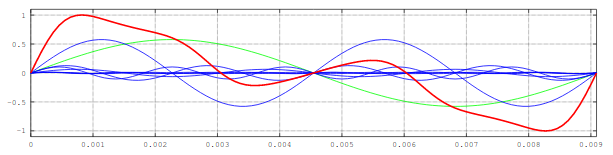
Para armar este timbre se utilizaron los parámetros \(f = 110\mbox{ Hz}\), \(a = 1\), \(F = \{1,2,3,4,5,6,7,8\}\) y \(A = \{0.58, 0.58, 0.064, 0.13, 0.10, 0.012, 0.012, 0.012\}\).
El timbre de cada instrumento musical tiene una impronta de armónicos tan característica que podemos reconocer si la misma nota la toca un piano o una guitarra, etc. El timbre del gráfico anterior es similar al de una flauta.
Muestreo
Cuando se quieren almacenar funciones continuas en forma discreta se realiza un muestreo de la misma.
Se llama muestrear a tomar una sucesión de valores de la función con un intervalo definido llamado frecuencia de muestreo \(f_m\).
Es decir, cuando muestreamos obtenemos una sucesión de valores \(v\) donde cada valor \(v_i\) se corresponde con un tiempo \(t_i\), y donde cada \(t_i = t_0 + \frac{i}{f_m}\).
Trabajo
Inicialización
Se pide implementar una función
void inicializar_muestras(float v[], size_t n);
que dado un vector de muestras v de longitud n inicialice todos
sus valores en cero.
Impresión
Se pide implementar una función
void imprimir_muestras(const float v[], size_t n, double t0, int f_m);
que dado un vector de muestras v de tamaño n generado a partir
de un tiempo t0 a una frecuencia de muestreo f_m lo imprima en
un formato adecuado.
Muestrear senoidal
Se pide implementar una función
void muestrear_senoidal(float v[], size_t n, double t0, int f_m, float f, float a);
que reciba un vector de muestras v de tamaño n y sume sobre él
el muestreo de una senoidal de frecuencia f y amplitud a a una
frecuencuencia de muestreo f_m iniciando en tiempo t0.
Muestrear armónicos
Se pide implementar una función
void muestrear_armonicos(float v[], size_t n, double t0, int f_m, float f, float a, const float fa[][2], size_t n_fa);
que dado un vector no inicializado v de tamaño n muestree a
frecuencia f_m iniciando en t0 los armónicos de una onda de
frecuencia fundamental f y amplitud a con frecuencias relativas e
intensidades de armónicos dados por el vector fa de tamaño
n_fa.
Por ejemplo, para la síntesis ya mostrada, el parámetro fa puede ser:
{
{1, 0.58},
{2, 0.58},
{3, 0.064},
{4, 0.13},
{5, 0.10},
{6, 0.012},
{7, 0.012},
{8, 0.012}
}
de longitud 8.
Para implementar esta función reutilizar funciones ya desarrolladas.
Pruebas
Escribir un programa que permita generar e imprimir la función de onda del ejemplo dado.
Verificar que la misma sea consistente con el gráfico presentado.
Entrega
Deberá entregarse:
El código fuente del programa desarrollado.
El gráfico de la onda sintetizada.
La entrega se realiza a través del sistema de entregas.
El ejercicio es de entrega individual.