Ejercicio obligatorio 2

Fecha de entrega: Domingo 9 de mayo

Introducción

Un polígono cerrado se puede definir como un vector \(P\) ordenado de \(n\) pares de coordenadas donde cada \(P_i\) es un punto \((x_i, y_i)\), donde cada segmento del polígono es un par \(S_i = \overline{P_i P_{i+1}}\) y el mismo se cierra con el segmento \(S_{n-1} = \overline{P_{n-1} P_0}\).

Si el polígono es convexo, es decir sus ángulos interiores son siempre menores a 180º, el mismo puede triangularse sencillamente, por ejemplo como un abanico:

por lo que si el problema fuera saber si algo está adentro o fuera del polígono esto puede resolverse comprobando si está dentro o fuera de cada uno de los triángulos que lo componen.

Para determinar si un punto \(P\) está dentro o fuera de un triángulo \(\overline{ABC}\) hay diferentes métodos:

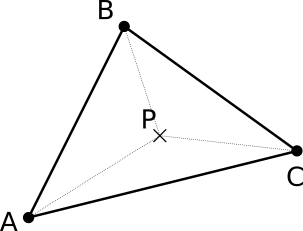
Uno es notar que el área del triángulo \(\overline{ABC}\) tiene que ser igual a la suma del área de los tres triángulos delimitados por \(P\), es decir \(\overline{ABP}\), \(\overline{BCP}\) y \(\overline{CAP}\).

Otro método usual (y más sencillo) es usando el producto vectorial, si se computa \((B - A) \times (P - A)\) (observación importante: siendo que todos los puntos están en el plano 2D, ¿dónde va a estar el resultado?) el signo del resultado depende de si P está de un lado del segmento \(\overline{AB}\) o del otro. Para que el punto esté dentro del triángulo los signos de realizar el producto con los tres segmentos deben ser iguales.

Implementación

Entrada en calor

Se pide implementar una función void trasladar(float poligono[][2], size_t n, float dx, float dy); que, dado un poligono modifique cada una de sus componentes mediante la adición del par (dx, dy). El poligono es un vector de n pares de forma {{X0, Y0}, {X1, Y1},... {Xn-1, Yn-1}}.

Entrada en calor 2

Se pide implementar una función void rotar(float poligono[][2], size_t n, double rad); que dado un poligono rote cada una de sus puntos rad radianes con respecto al origen de coordenadas.

Nota

Recordar que para rotar un punto \((x, y)\) un ángulo \(\theta\) se debe realizar la operación:

\(\begin{bmatrix}x' \\y' \\\end{bmatrix} = \begin{bmatrix}\cos \theta & -\sin \theta \\\sin \theta & \cos \theta \\\end{bmatrix}\begin{bmatrix}x \\y \\\end{bmatrix}\).

La operación puede descomponerse como:

\(x' = x \cos \theta - y \sin \theta\),

\(y' = x \sin \theta + y \cos \theta\).

Punto en triángulo

Se pide implementar una función bool punto_en_triangulo(float px, float py, float ax, float ay, float bx, float by, float cx, float cy); que diga si el punto de coordenadas (px, py) está dentro del triángulo delimitado por (ax, ay), (bx, by) y (cx, cy).

Punto en polígono

Se pide implementar una función bool punto_en_poligono(float poligono[][2], size_t n, float px, float py); que dado un poligono y un punto (px, py) diga si el punto está dentro del polígono o no.

Pruebas

Para el triángulo de vértices \([(1, 2), (3, 1), (2, 3)]\) puede observarse que están afuera los puntos \([(1.5, 1.5), (1.5, 2.6), (2.5, 2.5), (0.5, 2), (0, 0), (3.5, 0.5)]\) y que están adentro los puntos \([(1.1, 2), (2, 2.9), (2.9, 1.1), (2, 2), (2, 1.5), (1.5, 2.5), (2.5, 2), (1, 2), (3, 1), (2, 3)]\).

Para el polígono de vértices \([(1, 2), (3, 1), (6, 2), (6, 3), (4, 4), (2, 4)]\) están fuera los puntos \([(2, 1.4), (4.6, 1.5), (1, 1), (3, 4.1), (6.1, 0.5), (5, 3.6)]\) y están dentro los puntos \([(2, 2), (2, 3), (2, 1.6), (3, 1.5), (3, 2), (3, 3), (4, 1.5), (4, 2.5), (4, 4)]\).

Para el polígono de vértices \([(1, 2), (2, 4), (4, 4), (6, 3), (6, 2), (3, 1)]\) valen los puntos interiores y exteriores del polígono anterior. (Es el mismo polígono recorrido al revés.)

Llamar a las funciones punto_en_triangulo() y punto_en_poligono() con TODOS estos valores e imprimir un mensaje de error si alguno de los puntos no valida lo esperado.

Queda del lado del alumno probar las funciones trasladar() y rotar().

El main() del programa deberá correr los casos de prueba dados.

Entrega

Deberá entregarse el código fuente del programa desarrollado.

El programa debe compilar correctamente con los flags:

-Wall -Werror -std=c99 -pedantic

y validar los ejemplos dados.

La entrega se realiza a través del sistema de entregas.

El ejercicio es de entrega individual.