Trabajo Práctico 1
Fecha de entrega: Lunes 26 de julio
Introducción
Objetivo
El objetivo del presente trabajo práctico es la implementación de un clon del juego Peggle utilizando gráficos de líneas en SDL2.
El trabajo consiste en la resolución de un problema mediante el diseño y uso de TDAs y en la reutilización de los tipos y funciones desarrollados a lo largo del curso en trabajos anteriores.
Alcances
Mediante el presente TP se busca que el estudiante adquiera y aplique conocimientos sobre los siguientes temas:
Encapsulamiento en TDAs,
Uso de listas enlazadas,
Punteros a funciones,
Archivos,
Modularización,
Técnicas de abstracción,
además de los temas ya evaluados en trabajos anteriores.
Nota
Este trabajo es un trabajo integrador de final de cursada. En el mismo se van a aplicar todos los temas aprendidos y además se va a evaluar el diseño de la aplicación.
Es imprescindible entender los temas de TDA y modularización antes de empezar con el trabajo.
Es imprescindible diseñar el trabajo como etapa previa a la implementación.
Cualquier abordaje que pretenda empezar a codificar sin haber ordenado el trabajo primero está condenado a fracasar contra la complejidad del problema.
Lógica del juego
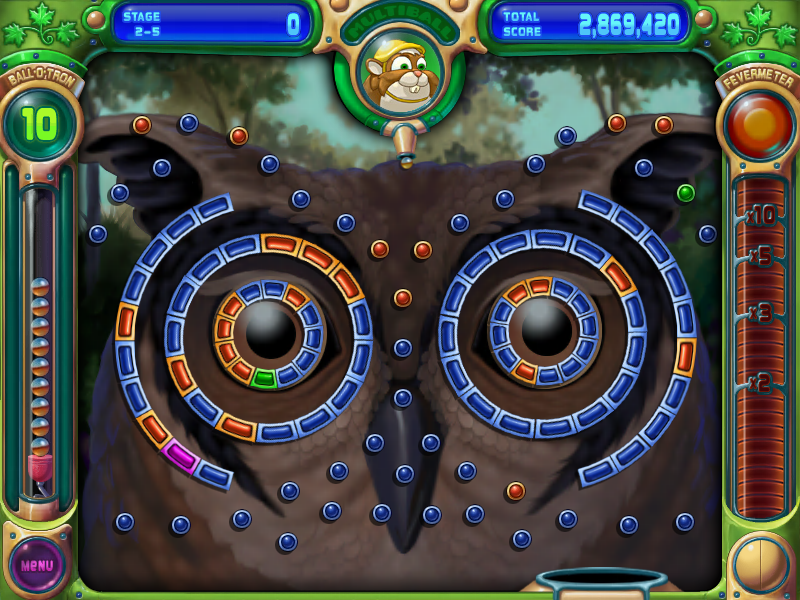
El juego Peggle es un juego estructurado en niveles. Cada uno de los niveles del juego se desarrolla dentro de un recuadro de la pantalla en el cual hay obstáculos de diferente geometría y comportamiento. En cada turno el jugador dispara una bola desde la parte superior de la pantalla, la cual cae e interactúa con los obstáculos hasta finalmente caer por debajo. Durante su caída rebotará sobre los diferentes obstáculos, cambiando en ello su dirección. Los obstáculos son de diferente tipo, los obstáculos grises son inmunes a la bola, pero los demás al ser tocados por la bola son marcados. Al final de cada turno se eliminan los obstáculos tocados por la bola. El nivel se completa cuando se hayan eliminado todos los obstáculos de color naranja.
En principio cada vez que se impacta contra un obstáculo azul o verde se suman 10 puntos, mientras que cuando se impacta contra un obstáculo naranja se suman 100 puntos. Pero además se contabiliza la cantidad de obstáculos naranjas que se impactan: Después de impactar 10 obstáculos naranjas los puntos se multiplicarán por dos, después de 15 por 3, después de 19 por 5 y, finalmente, después de 21 obstáculos naranjas impactados se multiplicarán los puntos por 10.
Cada nivel se empieza con la posibilidad de disparar 10 bolas. Si se impacta a uno de los obstáculos verdes se agregará una bola adicional. Si el turno finalizara sin tocar ninguno de los obstáculos a eliminar se anulará el turno sin perder la bola utilizada.
Si la bola quedara detenida en los obstáculos se disparará la eliminación de los obstáculos tocados aunque no haya terminado aún el turno para asegurar que la misma se libere.
Cuando se completa un nivel se pasa al nivel siguiente hasta ganar todos los niveles. El comportamiento original del juego es que cuando se agota la provisión de bolas se reinicia el nivel actual; para esta implementación se acepta tanto la implementación del comportamiento original como una implementación con bolas infinitas tal que nunca se reinicie un nivel.
Especificación
Detalles
Nota
Se provee el archivo config.h con la especificación de todas las
constantes que se mencionan.
Pantalla
El origen de coordenadas de pantalla es arriba a la izquierda. Las equis crecen hacia la derecha, las yes hacia abajo.
Física
El juego se ejecuta a la tasa de JUEGO_FPS cuadros por segundo, de donde se
puede calcular inmediatamente el DT, que es la duración de cada cuadro.
La bola se disparará con velocidad inicial BOLA_VI afectada por el ángulo en
el que se hace el disparo.
Cuando la bola esté cayendo sólo será afectada por la aceleración de la
gravedad G que actúa positiva sobre el eje y.
Además del problema dinámico clásico se agrega una corrección de fuerzas
viscosas por lo que en cada paso de tiempo la velocidad debe ser reducida por
la fracción indicada por ROZAMIENTO.
Choques
El área en la cual puede estar la bola está delimitada por MIN_X, MAX_X,
MIN_Y y MAX_Y. Tomar en cuenta que la bola tiene un radio BOLA_RADIO, por
lo que si la bola se representa por su centro ese radio debe ser considerado.
Si la bola pega contra las paredes izquierda, derecha o de arriba del área de juego la misma debe rebotar perfectamente. Si la bola pega contra la pared de abajo se termina el turno.
La bola pegará contra un obstáculo cuando la distancia de su centro al polígono
del obstáculo sea menor a BOLA_RADIO. Cuando esto ocurra la bola rebotará y,
además, su velocidad se afectará por la fracción definida en PLASTICIDAD.
Es decir, los choques contra las paredes son elásticos mientras que los choques contra los obstáculos disipan energía y frenan a la bola.
Se provee una función y una primitiva:
- Distancia a polígono:
La primitiva
double poligono_distancia(const poligono_t *p, float cx, float cy, float *norm_x, float *norm_y);recibe un polígonop, un punto (cx,cy) y devuelve la distancia del punto al polígono por el nombre y las componentes (norm_x,norm_y) de la normal al polígono en el punto más cercano.Esta primitiva permite evaluar si hay un impacto y la dirección contra la que debe rebotar la bola.
- Rebote contra un objeto:
La función:
void reflejar(float norm_x, float norm_y, float *cx, float *cy, float *vx, float *vy);recibe una normal (norm_x,norm_y), un punto (cx,cy) y una velocidad (vx,vy) y computa el rebote contra un objeto con esa normal modificando tanto el punto como la velicidad.
Geometrías
Por construcción de la función que obtiene las normales en los rebotes, todos los polígonos tienen que estar definidos recorriendo sus puntos en forma horaria.
Para los obstáculos de geometría círculo, los cuales poseen las coordenadas
\((x, y)\) del centro y un radio, debe definirse un poligono_t con una
determinada cantidad de puntos (por ejemplo 20) que representen puntos de un
círculo.
Nota
Notar que para generar un poligono_t desde puntos sueltos puede crearse
un polígono vacío con poligono_crear(NULL, 0) y luego agregarle puntos de
a uno.
Además notar que todos los objetos pueden crearse centrados en el origen,
horizontales, y luego ser rotados con poligono_rotar() y desplazados con
poligono_trasladar() según los parámetros deseados.
Los obstáculo de geometría de rectángulo poseen una coordenada \((x, y)\) de su centro y un ancho y un alto hacia los lados, además de un ángulo de rotación. Es decir, un polígono de cuatro puntos.
Movimiento
Advertencia
¡¡¡Se modificó la definición del movimiento horizontal con respecto al EJ4, se retiró un parámetro innecesario!!!
Los obstáculos con movimiento circular tienen 3 parámetros: un centro \((x, y)\) y una velocidad, dada en radianes por segundo. El obstáculo debe ser rotado en cada paso de tiempo con respecto a ese centro una cantidad dada para alcanzar la velocidad pedida.
Nota
Teniendo las primitivas poligono_trasladar() y poligono_rotar() se
puede implementar una primitiva poligono_rotar_centrado(p, cx, cy, ang)
como una sucesión de llamadas: trasladar + rotar + trasladar.
Los obstáculos con movimiento horizontal tienen 3 parámetros (en este orden), \(x_1\), \(x_i\) y velocidad (se eliminó de la especificación \(x_0\)). Los objetos se mueven en el intervalo \([0, x_1]\) a la velocidad dada, estando esta especificada en píxeles por segundo. La posición \(x_i\) es la posición inicial. Es decir, el obstáculo inicialmente estará en \(x_i\), se moverá a la velocidad dada hasta alcanzar o el 0 o el \(x_1\) (dependiendo del signo de la velocidad), una vez alcanzado este límite empezará a moverse en el sentido contrario, repitiendo todo el tiempo el ir y venir en el intervalo \([0, x_1]\).
¿Modificar o volver a crear?
Cuando se estudie y se analicen los distintos componentes en la etapa de diseño podrá verse que algunos objetos tienen posiciones paramétricas en cada instante mientras que otros objetos están definidos sólo por sus coordenadas.
En cuanto a la eficiencia, en este problema, se considera lo mismo generar un polígono en cada iteración para dibujarlo y luego destruído como tener siempre el mismo polígono e ir desplazándolo en cada iteración.
En algunos casos, como por ejemplo el dibujado de la bola, probablemente sea más sencillo generar su polígono cada vez que preocuparse por trasladarlo consistentemente con la evolución de sus parámetros.
Trabajo
El enunciado de este trabajo será breve, no se introducirá ningún concepto
nuevo. Ya tenemos implementado nuestro TDA poligono_t y tenemos desarrollada
parte de la lógica de lectura de obstáculos, también funciones para el manejo
del motor físico, en los códigos ya dados se encuentra además la lógica de
lectura de un archivo de niveles, y se encuentra provista por la cátedra la
implementación del TDA lista enlazada.
El problema que se plantea en este trabajo deberá ser resuelto con las herrramientas ya adquiridas, extendiendo de forma consistente los TDAs ya planteados y diseñando los TDAs nuevos que hagan falta. Se evaluará además el correcto uso de los TDAs respetando la abstracción y el "modelo" de Alan-Bárbara.
Aplicación
Se pide diseñar una aplicación que pueda ser ejecutada como:
$ ./peggle niveles.bin
que permita jugar al juego Peggle para ese conjunto de niveles, con toda la lógica del problema y que sea capaz de informar al usuario de los eventos, su puntaje parcial (del nivel), acumulado, etc.
Encapsulamiento
Se deben implementar TDAs donde se considere que es necesario.
A priori es obligatorio que los obstáculos conformen un TDA y que el mismo sea
consumido desde la lógica del juego. Es decir, el obstáculo es el obstáculo y
sabrá desplazarse, marcarse, dibujarse sobre un SDL_Renderer, etc. pero no
decidirá la lógica de alto nivel del juego.
Todos los obstáculos que se están jugando en un nivel deberán estar almacenados en una lista enlazada de la implementación provista por la cátedra. Notar que en cada iteración del problema se realizan operaciones sistemáticas sobre cada uno de los obstáculos: Moverlos, verificar que no haya una colisión con la bola (y si la hay marcarlo), dibujarlos, etc. y también hay operaciones que se realizan en momentos decisivos, como por ejemplo eliminar todos los obstáculos marcados, o seleccionar para el juego los obstáculos de otro nivel.
Nota
En todos los casos cuando se habla de TDA se habla de tipos encapsulados donde el detalle de implementación interna no está disponible para el consumidor.
Es decir, la lógica del juego deberá interactuar con listas de obstáculos donde tanto la lista como el obstáculo son tipos oscuros que se manipulan a través de sus primitivas.
Hay más objetos del juego que pueden ser diseñados como TDAs.
Estados
Notar que el juego tiene diferentes etapas, por ejemplo, el momento en el que se está esperando que el usuario dispare la bola, y el momento en el que la bola está interactuando. Puede haber otros estados en los cuales se muestren mensajes específicos, etc.
Diseñar de forma elegante los diferentes estados y las transiciones de un estado al siguiente. Utilizar tipos enumerativos, booleanos, etc.
Alcance
El alcance inicial del juego es el especificado y una buena implementación del mismo es suficiente para alcanzar la máxima nota. La prioridad es resolver completa esta funcionalidad descrita para terminar con eso la materia.
Ahora bien, por simplificar el enunciado se dejaron afuera de la especificación muchos detalles del juego original que hacen a la jugabilidad y que pueden ser implementados como puntos optativos de querer.
Algunas cosas que se extrañan en esta implementación y que pueden ser agregadas sin mucho trabajo adicional:
Dibujar una ayuda con la trayectoria que tendría el tiro,
Implementar el recuperador de bolas que hace ganar bolas adicionales. Notar que el mismo es un obstáculo con movimiento horizontal,
Hacer que la posición del mouse coincida con la trayectoria de la bola,
entre otras.
Material
Implementaciones
Se cuenta con la implementación de lista enlazada mandada por correo el día 28/06.
Se cuenta con el esqueleto de SDL2 y el archivo config.h enviado por correo
el día 28/06.
Se proveen las siguientes funciones generales:
/*
Para encontrar la distancia de un punto a una recta se proyecta el punto
ortogonalmente sobre la recta.
El producto [(X.P) / (X.X)] X es la proyección del punto P sobre X.
El coeficiente entre corchetes será la proporción de P sobre X.
Como estamos trabajando con segmentos de recta, si el coeficiente es menor a
cero o mayor a uno nos caímos del segmento.
*/
void punto_mas_cercano(float x0, float y0, float x1, float y1, float xp, float yp, float *x, float *y) {
float ax = xp - x0;
float ay = yp - y0;
float bx = x1 - x0;
float by = y1 - y0;
float alfa = producto_interno(ax, ay, bx, by) / producto_interno(bx, by, bx, by);
if(alfa <= 0) {
*x = x0;
*y = y0;
}
else if(alfa >= 1) {
*x = x1;
*y = y1;
}
else {
*x = alfa * bx + x0;
*y = alfa * by + y0;
}
}
/*
Reflejamos según P' = P - 2 D(P.D)
*/
void reflejar(float norm_x, float norm_y, float *cx, float *cy, float *vx, float *vy) {
float proy = producto_interno(norm_x, norm_y, *vx, *vy);
if(proy >= 0)
return;
*vx -= 2 * norm_x * proy;
*vy -= 2 * norm_y * proy;
// Además empujamos a la bola hacia afuera para que no se pegue
*cx += norm_x * 0.1;
*cy += norm_y * 0.1;
}
Y la siguiente primitiva del poligono_t:
double poligono_distancia(const poligono_t *p, float xp, float yp, float *nor_x, float *nor_y) {
double d = 1 / 0.0;
size_t idx = 0;
for(size_t i = 0; i < p->n; i++) {
float xi, yi;
punto_mas_cercano(p->vertices[i][0], p->vertices[i][1], p->vertices[(i + 1) % p->n][0], p->vertices[(i + 1) % p->n][1], xp, yp, &xi, &yi);
double di = distancia(xp, yp, xi, yi);
if(di < d) {
d = di;
idx = i;
}
}
float nx = p->vertices[(idx + 1) % p->n][1] - p->vertices[idx][1];
float ny = p->vertices[idx][0] - p->vertices[(idx + 1) % p->n][0];
float dn = distancia(nx, ny, 0, 0);
nx /= dn;
ny /= dn;
*nor_x = nx;
*nor_y = ny;
return d;
}
La documentación de las mismas se encuentra previamente en el enunciado.
Niveles
Se proveen diferentes niveles del juego disponibles en: archivos_20211_tp1_niveles.tar.gz
El archivo peggle.bin contiene todos los niveles juntos, mientras que los
demás son niveles individuales.
Dinámica esperada
El siguiente video muestra tiros sucesivos con el cañón en el ángulo máximo para el nivel 1-1:
El siguiente video muestra la dinámica del movimiento circular en el nivel 2-5:
El siguiente video muestra la dinámica del movimiento horozintal en el nivel 3-4:
Todas estas muestras deben servir para validar lo desarrollado, la dinámica de movimiento y de rebotes debe ser la misma.
Valgrind
En el caso de una aplicación construída con SDL2 se hace complejo el uso de Valgrind porque esta biblioteca tiene desprolijidades en su implementación que hacen que Valgrind tire múltiples errores y estos errores a la tasa que marquen los FPS del juego. Por eso para poder testear con Valgrind sobre el código desarrollado tenemos que suprimir los errores que son relativos a SDL2.
Se provee el siguiente archivo de supresiones para Valgrind:
suppressions_20211_tp1.supp
Con este archivo descargado Valgrind puede ser invocado como:
$ valgrind --suppressions=suppressions_20211_tp1.supp --leak-check=full ./peggle peggle.bin
con lo que el programa se ejecutará suprimiendo los millones de erroes de SDL2.
Al haber errores y haberlos suprimido el reporte no será del todo satisfactorio, y va a haber memoria en el heap y elementos marcados como "still reachable". El siguiente es un reporte de ejemplo:
==27213== Memcheck, a memory error detector
==27213== Copyright (C) 2002-2017, and GNU GPL'd, by Julian Seward et al.
==27213== Using Valgrind-3.13.0 and LibVEX; rerun with -h for copyright info
==27213== Command: ./peggle peggle.bin
==27213==
==27213==
==27213== HEAP SUMMARY:
==27213== in use at exit: 196,326 bytes in 1,058 blocks
==27213== total heap usage: 32,817 allocs, 31,759 frees, 118,233,488 bytes allocated
==27213==
==27213== LEAK SUMMARY:
==27213== definitely lost: 0 bytes in 0 blocks
==27213== indirectly lost: 0 bytes in 0 blocks
==27213== possibly lost: 0 bytes in 0 blocks
==27213== still reachable: 2,037 bytes in 10 blocks
==27213== suppressed: 194,289 bytes in 1,048 blocks
==27213== Reachable blocks (those to which a pointer was found) are not shown.
==27213== To see them, rerun with: --leak-check=full --show-leak-kinds=all
==27213==
==27213== For counts of detected and suppressed errors, rerun with: -v
==27213== ERROR SUMMARY: 0 errors from 0 contexts (suppressed: 1018824 from 25)
Notar que pese a que se señala más de un millón de errores, el reporte de
pérdidas dice que no hay bloques ni definitiva, ni indirecta ni posiblemente
perdidos. Además el reporte, pese a haber sido corrido con --leak-check=full
no muestra ningún error en nuestro propio código.
Se busca que el reporte tenga estas características.
Ahora bien, prestar atención porque ignorar los errores de still reachable
puede enmascarar errores como por ejemplo no haber llamado a fclose() entre
otros.
Nota
Ejecutar con Valgrind implica a poner a un programa a analizar cada cosa que hace nuestro programa. Con un programa pesado en cantidad de operaciones como el nuestro, el programa va a andar muy lento.
La idea es correr con Valgrind como un chequeo a realizar, pero no todo el tiempo durante del desarrollo.
Para liberar la carga, sólo durante las corridas de Valgrind, se puede
reducir el valor de JUEGO_FPS a un valor que lo haga más manejable. Esto
va a romper la física del juego, pero al menos va a permitir testear más
intensivamente la memoria.
Entrega
Requisitos
Los únicos requisitos son que el programa resuelva correctamente la funcionalidad pedida y que lo haga utilizando TDAs con un diseño planificado a conciencia. Si hacés eso nada puede salir mal.
Entregables
Deberá entregarse:
El código fuente del trabajo debidamente documentado.
El archivo
Makefilepara compilar el proyecto.
Nota
El programa debe:
estar programado en C,
estar completo,
compilar...
sin errores...
sin warnings,
correr...
sin romperse...
sin fugar memoria...
resolviendo el problema pedido...
Trabajos que no cumplan con lo anterior no serán corregidos.
La entrega se realiza a través del sistema de entregas.
El ejercicio es grupal permitiéndose grupos de hasta 2 integrantes.
Si elegís hacer el trabajo en grupo te pedimos que nos avises o por mail o por Discord quién es tu compañero de grupo así lo cargamos en el sistema de entregas. (Si el grupo sufriera alteraciones avisanos también.)