Ejercicio obligatorio 1
Fecha de entrega: Viernes 24 de septiembre
Introducción
En la computación gráfica un método muy poderoso para renderizar (generar imágenes a partir de) escenas consiste en disparar rayos desde la posición en la cual se encuentra el observador y ver cómo la trayectoria de cada uno de estos rayos intersecta a los diferentes objetos. Este método se llama ray tracing (trazado de rayos).
Como lo que se quiere generar es una imagen, y en la computación gráfica las imágenes son un conjunto discreto de pixels, con determinada cantidad de ellos a lo ancho \(w\) y a lo alto \(h\) no es que se disparan rayos en todas las direcciones posibles sino en direcciones que tienen relación con el sentido en el que se está mirando y el ángulo de visión, de tal manera de que cada uno de los rayos atraviese a cada uno de los pixeles de la imagen. De los objetos que ese rayo atraviese dependerá el valor de ese pixel.
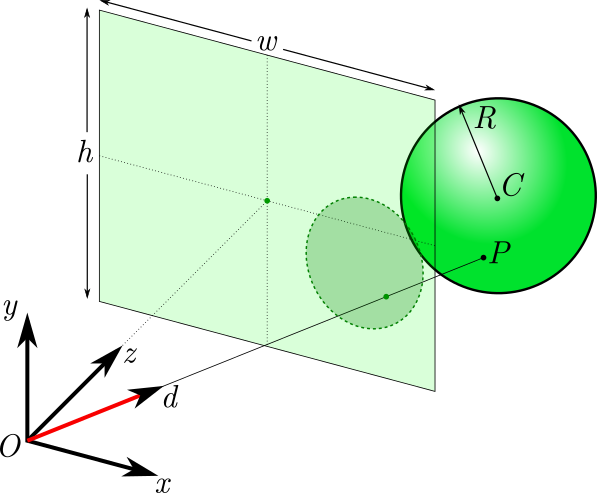
En nuestra escena tenemos a nuestro observador \(\vec O\) el cual mira en la dirección del eje \(\hat z\), siendo los otros dos ejes restantes los que nos dan la referencia de cómo está orientado. Cada uno de los rayos que se disparan tienen una dirección normalizada \(\hat d\). Entonces, paramétricamente cualquier punto sobre el rayo tendrá una posición \(\vec{r}(t) = \vec O + t \hat d\) con el parámetro \(t \geq 0\). Si por simplicidad hacemos coincidir al observador con el origen esta ecuación se convierte en \(\vec{r}(t) = t \hat d\).
Ahora bien, nuestra escena contiene una esfera de centro \(\vec C\) y radio \(R\). Sabemos que todos los puntos de una esfera están a distancia radio del centro, por lo que los puntos que cumplan con \((\vec P - \vec C) \cdot (\vec P - \vec C) = R^2\) serán los puntos de su superficie.
Un rayo intersectará a una esfera si es posible encontrar un valor de \(t\) para el cual \(\vec r(t) = \vec P\). Realizando el reemplazo de una ecuación en la otra se ve que resulta \((\vec O + t \hat d - \vec C) \cdot (\vec O + t \hat d - \vec C) = R^2\) y operando obtenemos \(t^2 (\hat{d} \cdot \hat{d}) + 2 (\vec O - \vec C) t \hat d + (\vec O - \vec C) \cdot (\vec O - \vec C) - R^2 = 0\), ecuación cuadrática sobre \(a t^2 + b t + c = 0\) con soluciones ya conocidas.
Nota
En el siguiente párrafo desarrollaremos el cómputo de \(t\) pero eso no va a ser usado en este ejercicio. Del mismo modo que incluimos el valor de \(\vec O\) que ya dijimos que para este problema va a ser tomado como el cero, por lo que puede eliminarse de la ecuación.
Como \(\hat d\) es un versor, su producto interno es unitario por lo que el término \(a = 1\). Definamos \(\beta = (\vec C - \vec O) \cdot \hat d\) y \(\delta = \beta^2 - (\vec C - \vec O)\cdot(\vec C - \vec O) + R^2\) entonces las soluciones de la ecuación estarán dadas por \(t = \beta \pm \sqrt\delta\) y, como es usual, la existencia de dichas soluciones dependerá del signo de \(\delta\) (el discriminante). Si dicho término es positivo entonces hay intersección entre el rayo y la esfera, si no, no. Luego, de existir soluciones nos interesan sólo las que sean positivas (es decir, están adelante del rayo y no a espaldas) y la menor de ellas, es decir, si \(\beta - \sqrt\delta > 0\) esa será la solución, y si no será \(\beta + \sqrt\delta\), y si ambas son negativas entonces no hay intersección.
Retomando el ejercicio, con las simplificaciones de nuestro problema y asumiendo que la esfera está siempre frente al rayo, saber si el rayo toca a la esfera implica verificar
El formato PBM
Como ya dijimos, vamos a generar imágenes digitales, es decir, una matriz de determinado ancho y alto en la cual cada unidad es el pixel.
Para simplificar el proceso utilizaremos uno de los formatos del paquete Netpbm que permite generar gráficos de forma muy sencilla. Particularmente en este trabajo utilizaremos la variante ASCII del formato PBM (portable bitmap).
Un archivo PBM es la secuencia de: El encabezado P1, seguido de las dimensiones en ancho y alto de la imagen, seguido de una secuencia de ceros y unos según el pixel sea blanco o negro respectivamente, recorridos de izquierda a derecha y de arriba a abajo.
Como una imagen vale mil palabras, por ejemplo el archivo:
P1
20 7
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 0 0 0 0 1 1 0 0 0 0 1 1 0 0 1 1 0 0 1
1 0 1 1 0 1 1 0 1 1 1 1 1 1 0 1 1 1 0 1
1 0 0 0 0 1 1 0 0 0 0 1 1 1 0 1 1 1 0 1
1 1 1 1 0 1 1 1 1 1 0 1 1 1 0 1 1 1 0 1
1 0 0 0 0 1 1 0 0 0 0 1 1 1 0 1 1 1 0 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
genera la imagen (ampliándola varias veces):

No hace falta que los pixeles estén estructurados como en una matriz, puede haber uno por línea y el formato es igualmente válido.
Álgebra
Se pide programar una función
float producto_interno(float x1, float y1, float z1, float x2, float y2, float z2);
que devuelva el producto interno \(X_1 \cdot X_2 = (x_1, y_1, z_1) \cdot (x_2, y_2, z_2)\).
Se pide programar una función
float norma(float x, float y, float z); que devuelva la norma del
vector \((x, y, z)\).
Intersección de esferas
Dadas las siguientes definiciones:
#define CX 0.5
#define CY 0.75
#define CZ 1.9
#define R 0.8
Programar una función
int intersecta_esfera(float dx, float dy, float dz); que
verifique si la dirección unitaria \(\hat d = (d_x, d_y, d_z)\) intersecta
a la esfera de centro (CX, CY, CZ) y radio R. La función debe devolver 1
de haber intersección y 0 en caso de no haberla.
Aplicación
Teniendo las siguientes definiciones:
#define ANCHO 640
#define ALTO 480
#define FOV 90
y las funciones anteriores desarrollar un programa que genere la salida PPM del ray tracing con la escena de nuestra esfera.
Se debe desarrollar una imagen de ANCHO por ALTO. Como nuestro punto de
vista está en el origen de coordenadas, entonces el centro de la imagen estará
en la mitad de las dimensiones. Dicho de otra forma, las coordenadas de los
pixeles en \(x\) irán en el intervalo
\([-\mbox{ancho} / 2, \mbox{ancho}/2)\) mientras que
\(y \in [-\mbox{alto}/2, \mbox{alto}/2)\).
Para cada uno de los pixeles \((x, y)\) se debe computar la dirección
\(\hat d\). Para esto se utiliza el parámetro FOV, expresado en grados,
que representa el campo de visión, es decir, cuál es el ángulo del ojo del
observador. Con la información de este ángulo y la del ancho de la imagen se
puede establecer la coordenada \(z\) que completa la terna como
con esto se obtienen las componentes de la dirección \(d = (x, y, z)\). Ahora bien, notar que para obtener el versor \(\hat d\) las mismas deben ser normalizadas.
El valor de cada uno de los pixeles de la imagen dependerá de si existe intersección entre la dirección y la esfera o no.
Graficación
Se pide abrir la imagen generada con un visor de imágenes de su preferencia (gimp, eog, etc.).
Convertir la imagen a PNG o JPG o realizar una captura de pantalla donde se vea la imagen abierta.
Validación
La imagen generada por la cátedra con los mismos parámetros es la siguiente

validar que la salida generada sea consistente con respecto a esta imagen de referencia.
Entrega
- Deberá entregarse:
El código fuente del programa desarrollado.
La imagen generada o la captura correspondiente en formato JPG o PNG.
La entrega se realiza a través del sistema de entregas.
El ejercicio es de entrega individual.