Ejercicio obligatorio 2
Fecha de entrega: Domingo 3 de octubre
Introducción
Nota
Se conoce del EJ1 la ecuación completa de la intersección rayo esfera.
Refrescar ese desarrollo porque es necesario para este ejercicio.
Si se quisiera resolver la iluminación en una escena se deberían resolver las ecuaciones del transporte de luz las cuales son inabarcables computacionalmente, por eso es que, como en muchas áreas de la física, se recurre a modelos simplificados.
En los diferentes trabajos vamos a construir el modelo de iluminación de Phong, que propone que la iluminación de cada objeto es la combinación del aporte de diferentes componentes sencillos de calcular.
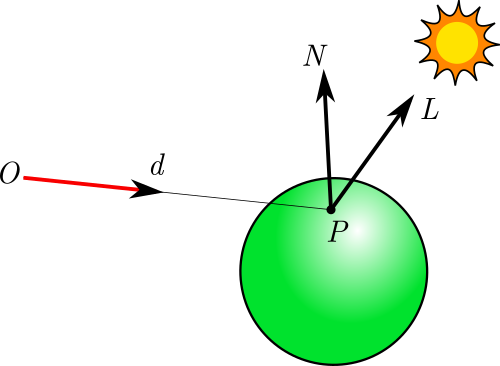
El observador \(\vec O\) mira en la dirección \(\hat d\) e intersecta al objeto en la posición \(\vec P\) (con \(\vec P = \vec O + t \hat d\)). En ese punto \(\vec P\) el objeto tiene una normal \(\hat N\), y además existe una fuente de luz distante en la dirección \(\hat L\).
Si bien el modelo de Phong plantea más términos diremos en este momento que la iluminación del punto \(\vec P\) depende de dos cosas: La primera es de una iluminación de ambiente que existe de base y que va a iluminar sin dirección definida a todos los materiales. La segunda es una iluminación difusa que va a depender de cómo la luz impacte al material, cuanto más alinada esté la normal con la fuente de luz más brillante será.
Es decir:
donde \(I\) es la intensidad de luz en el punto \(\vec P\), \(I_a\) es la intensidad de la iluminación ambiente y \(I_i\) es la intensidad de la fuente de luz.
El aporte de la iluminación ambiente se da siempre. Ahora bien, el aporte de la iluminación difusa depende de que haya visibilidad del punto \(\vec P\) en la dirección \(\hat L\). Si mirando en ese sentido ningún objeto se interpusiera entonces \(\delta_s\) valdrá 1, en cambio si hubiera algún objeto entonces el mismo haría sombra y \(\delta_s\) valdría 0. En ese caso sólo estará presente la componente ambiental dado que al no incidir la luz no habría componente difusa en ese lugar.
El formato PGM
El formato PGM (portable graymap) es el formato de Nepbm para representar imágenes en escala de grises.
Un archivo PGM es la secuencia de: El encabezado P2, seguido de las dimensiones de ancho y alto, seguido del valor máximo, seguido de una secuencia de números entre 0 y el máximo según el valor del pixel. El valor 0 será negro mientras que el valor máximo será blanco, siendo grises los valores intermedios.
Por ejemplo el siguiente archivo:
P2
20 7
15
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 3 3 3 3 0 0 7 7 7 7 0 0 11 11 0 0 15 15 0
0 3 0 0 3 0 0 7 0 0 0 0 0 0 11 0 0 0 15 0
0 3 3 3 3 0 0 7 7 7 7 0 0 0 11 0 0 0 15 0
0 0 0 0 3 0 0 0 0 0 7 0 0 0 11 0 0 0 15 0
0 3 3 3 3 0 0 7 7 7 7 0 0 0 11 0 0 0 15 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
genera la imagen (ampliándola varias veces):

Nosotros vamos a trabajar siempre con un valor máximo de 255, que suele
ser lo estándar en imágenes.
Implementación
Vectores
Para representar una terna de coordenadas utilizaremos vectores de 3 elementos, correspondientes a \((x, y, z)\).
Implementar la función
float producto_interno(const float a[3], const float b[3]); que devuelva el
resultado de \(\vec a \cdot \vec b\).
Implementar la función float norma(const float a[3]); que devuelva la norma
del vector a.
Implementar la función void normalizar(float a[3]); que normalice al vector
a.
Implementar la función
void resta(float r[3], const float a[3], const float b[3]); que compute
\(\vec r = \vec a - \vec b\), es decir, guarde en r la resta entre a y
b.
Implementar la función
void interpolar_recta(float p[3], const float o[3], const float d[3], float t);
que compute \(\vec P = \vec O + t \hat d\), es decir guarde en p la
interpolación de la recta dada por el origen o y la dirección d en la
distancia t.
Esferas
Representaremos a una esfera como un centro \(\vec C\) y un radio \(R\), donde el centro es una terna de coordenadas y el radio un valor.
Teniendo definido
#include <float.h>
#define INFINITO FLT_MAX
Implementar la función
float distancia_esfera(const float c[3], float r, const float o[3], const float d[3]);
que compute la distancia (\(t\)) entre la esfera de centro \(\vec C\) y
radio \(R\) y la recta dada por \(\vec O + t \hat d\). Si no hubiera
intersección entre la recta y la esfera devolver INFINITO.
Implementar la función
void normal_esfera(float normal[3], const float c[3], float r, const float p[3]);
que guarde en normal el valor de \(\hat N\), la normal de la esfera de
centro c y radio r en el punto p. Notar que la normal es un versor.
Transporte de luz
Se tienen definidos
#define IA 5
#define II 255
const float luz[3] = {0.2873478855663454, 0.9578262852211513, 0};
const float centros[][3] = {
{-.4, .75, 1.55},
{-.55, -.4, 2},
{3, 1.5, 4},
{3, 1.5, 5},
{3, -1.5, 4},
{3, -1.5, 5},
};
const float radios[] = {
.3,
.85,
.4,
.4,
.4,
.4,
};
que son la intensidad ambiente IA, la intensidad de la luz II, la dirección
de la fuente de luz luz, los centros \(\vec C\) de las esferas con
sus respectivos radios \(R\).
Implementar la función
int computar_intensidad(const float cs[][3], const float rs[], size_t n_esferas, const float luz[3], const float o[3], const float d[3]);
que devuelva el valor de intensidad \(I\) correspondiente a la dirección
\(\hat d\) desde el origen \(\vec O\) para la escena con las n_esferas
esferas de centros cs y radios rs, la posición de la luz dada
y los valores de intensidad previamente definidos. Si el valor de intensidad resultante es
mayor a 255 se debe devolver 255 (que es el máximo).
Aplicación
Desarrollar un programa que genere una imagen PGM para la escena dada, con la misma estructura y constantes que el EJ1 ya realizado.
Nota
Al llamar a computar_intensidad() el origen o es siempre el cero de
coordenadas y la dirección d es un versor.
Graficación
Se pide abrir la imagen generada con un visor de imágenes de su preferencia (gimp, eog, etc.).
Convertir la imagen a PNG o JPG o realizar una captura de pantalla donde se vea la imagen abierta.
Validación
La imagen generada por la cátedra con los mismos parámetros es la siguiente

validar que la salida generada sea consistente con respecto a esta imagen de referencia.
Entrega
- Deberá entregarse:
El código fuente del programa desarrollado.
La imagen generada o la captura correspondiente en formato JPG o PNG.
La entrega se realiza a través del sistema de entregas.
El ejercicio es de entrega individual.