Ejercicio obligatorio 3

Fecha de entrega: Domingo 31 de octubre

Introducción

Nota

Este ejercicio no suma parámetros nuevos a la ecuación desarrollada en el EJ2, sólo cambia sutilmente cómo se operan dichos parámetros.

Hasta el momento modelamos el mundo como si el mismo fuera monocromático, por lo que nuestros rayos de luz sólo computaban una intensidad total sobre el "color" blanco. En el mundo real los rayos de luz tienen una determinada longitud de onda, y a la vez los materiales de las cosas tienen la capacidad de absorber más o menos determinadas longitudes de onda. Dicho de otro modo, las fuentes de luz tienen un determinado color que es el de las frecuencias que emiten, y además los objetos tendrán un determinado color que es el de las frecuencias que reflejan.

En computación gráfica solemos representar a los colores según tres componentes de colores según su intensidad de rojo, verde y azul (RGB). Si bien estas tres componentes no pueden generar todo el espectro, son una buena aproximación. Entonces la longitud de onda de un rayo de luz se codifica según una intensidad para una terna de colores luz primarios.

A partir de ahí entonces las fuentes de luz tendrán un color y una intensidad que se especificará como los valores de sus componentes RGB y luego los objetos tendrán un color que se especificará como los valores de sus componentes RGB. Además cada objeto tendrá una determinada respuesta a la iluminación ambiental \(\vec I_a\) y a la iluminación difusa, según los coeficientes \(k_a\) y \(k_d\) respectivamente.

Considerando múltiples fuentes de luz, cada una con una intensidad \(\vec I_i\) y una dirección \(\vec L_i\) (hablaremos de la dirección más adelante) la ecuación para el color recibido en un punto de la superficie se convierte en:

\[\vec C = \vec I_a k_a + \sum_{\forall i} \delta_{si} [\vec I_i k_d (\hat L_i \cdot \hat N)].\]

Como primera cosa notar que las intensidades ahora son vectores, es decir, cada intensidad es ahora una terna \(\vec I = (I_R, I_G, I_B)\), notar que, al igual que hasta el momento también las direcciones son vectoriales, pero en ese caso son ternas sobre \((x, y, z)\), si bien ambos son vectores pertenecen a espacios diferentes.

Como segunda cosa notar que esta fórmula que calcula el color recibido se conforma por el color de luz que se recibe de parte de la iluminación ambiente y por el color de cada una de las fuentes de luz que incidan sobre el objeto y de los coeficientes que tenga el objeto para absorber o reflejar estas luces, pero hasta el momento no aparece el color del objeto en la ecuación.

El color reflejado por el material va a ser el producto componente a componente entre el color recibido \(\vec C\) y el color del material \(\vec M\):

\[\vec I = \vec C \odot \vec M = (C_R M_R, C_G M_G, C_B M_B)\]

Para finalizar, volvamos a las fuentes de luz. En la computación gráfica se suelen definir dos tipos de fuentes de luz: o puntuales o de rayos paralelos. Las fuentes puntuales emiten desde un determinado punto, mientras que las de rayos paralelos emiten desde un punto ubicado en el infinito por lo que se representan por una dirección. La fuente de luz del EJ2 se trataba de una fuente de rayos paralelos y estaba dada por una dirección \(\hat L\).

En el caso de una luz puntual, la misma está dada por una coordenada \(\vec C_L\) y no una dirección por lo que la dirección con respecto a algún punto \(\vec P\) puede obtenerse como \(\vec L = \vec C_L - \vec P\). Como siempre, \(\hat L = \frac{\vec L}{\lVert \vec L \rVert}\).

El formato PPM

El formato Portable Pixel Map (PPM) es el pináculo de la evolución del paquete Netpbm. El mismo permite la codificación de imágenes a color en un archivo sencillo.

El formato es similar al PGM ya analizado con la diferencia de que ahora por cada pixel en vez de tener un único valor de grises tendremos tres valores, uno para cada componente RGB del color.

Por ejemplo el siguiente archivo

P3
# Este es un ejemplo de PPM
4 4
# Asumimos que el máximo es siempre 255
255
#   Rojo                                     Verde
255   0   0   170  85   0    85 170   0     0 255   0
170   0  85   141  85  85   113 170  85    85 255  85
 85   0 170   113  85 170   141 170 170   170 255 170
  0   0 255    85  85 255   170 170 255   255 255 255
#   Azul                                     Blanco

genera la siguiente imagen:

Resumiendo: El encabezado es P3, hay 3 valores numéricos por cada pixel.

Trabajo

vector_t y color_t

Se tienen definidos los siguientes tipos:

typedef struct {
    float x, y, z;
} vector_t;

typedef struct {
    float r, g, b;
} color_t;

que representan a un vector en \(\mathbb R^3\) y a un color RGB respectivamente.

Cada componente de color se representa por un valor donde 0 significa ausencia y 1 significa que la componente está al máximo. Si una componente está en un valor superior a 1 se considera a fines prácticos como que estuviera al valor máximo y no debe ajustarse.

Al momento de generar cada pixel del archivo PPM el rango flotante 0..1 debe escalarse al rango entero 0..255 y los valores superiores a 1 deben truncarse a 255.

Otra vez sopa

Se pide implementar (algunas por segunda y otras por tercera vez) las siguientes funciones de vector_t:

float vector_producto_interno(vector_t a, vector_t b);
float vector_norma(vector_t a);
vector_t vector_resta(vector_t a, vector_t b);
vector_t vector_interpolar_recta(vector_t o, vector_t d, float t);
vector_t vector_normalizar(vector_t a);

las cuales son análogas a las ya implementadas en los EJ1 y EJ2.

Implementar la función color_t color_sumar(color_t c, color_t m, float p); que devuelve un nuevo color dado por \(\vec c + p \vec m\).

Implementar la función color_t color_absorber(color_t b, color_t c); que devuelve el color dado por \(\vec b \odot \vec c\), es decir el producto elemento a elemento de sus componentes RGB.

Implementar la función void color_imprimir(color_t c); que imprima por stdout las componentes RGB de un color en el formato esperado por PPM como valores enteros entre 0 y 255. Como ya se aclaró, cualquier valor del float superior a 1 se considerará como 255.

Esferas y luces

Se tienen las siguientes definiciones:

typedef struct {
    vector_t centro;
    float radio;

    color_t color;

    float ka, kd;
} esfera_t;

typedef struct {
    vector_t posicion; // Si es_puntual es una coordenada, si no una dirección
    color_t color;
    bool es_puntual;
} luz_t;

La primera representa a una esfera con su centro, su radio, su color y sus coeficientes ambiental y difuso, la segunda representa a una fuente de luz con su posición (la cual será una coordenada o una dirección dependiendo de si es puntual o no), su color y la indicación de si es puntual.

Se pide implementar una función esfera_t *esfera_crear(vector_t centro, float radio, color_t color, float ka, float kd); que cree una esfera con los parámetros dados.

Se pide implementar una función void esfera_destruir(esfera_t *esfera); que destruya la esfera dada previamente creada.

Se pide implementar una función luz_t *luz_crear(vector_t posicion, color_t color, bool es_puntual); que cree una fuente de luz con los parámetros dados.

Se pide implementar una función void luz_destruir(luz_t *luz); que destruya la luz dada previamente creada.

Otra vez sopa 2

Se pide implementar una función float esfera_distancia(const esfera_t *esfera, vector_t o, vector_t d, vector_t *punto, vector_t *normal); que compute la distancia del rayo dado por \(\vec o + t \hat d\) a la esfera, de no haber intersección debe devolverse INFINITO. En caso de devolver un número finito debe devolverse, además, por la interfaz el punto de intersección a través del parámetro punto y la normal en dicho punto a través del parámetro normal.

Un (mini) arreglo dinámico

Se tiene definida la estructura:

struct {
    void **v;
    size_t n;
} arreglo_t;

el cual representa un arreglo que contiene n elementos contenidos en v, implementar una función bool arreglo_agregar(arreglo_t *a, void *e); que agregue un elemento e al final del arreglo a. La función debe redimensionar a v e incrementar n. De todo salir bien debe devolver true de fallar debe dejar a a tal cual como lo recibió y devolver false.

Finalmente

Implementar la función color_t computar_intensidad(const arreglo_t *esferas, const arreglo_t *luces, color_t ambiente, vector_t o, vector_t d); que devuelva la intensidad para el arreglo de esferas, luces y esa iluminación ambiente en el rayo representado por o y d.

Aplicación

Se provee completa la implementación del programa principal:

int main(void) {
    arreglo_t luces = {NULL, 0};
    arreglo_t esferas = {NULL, 0};

    color_t ambiente = {.05, .05, .05};

    assert(arreglo_agregar(&luces, luz_crear(vector_normalizar((vector_t){0, 1, 0}), (color_t){.2, .2, .2}, false)));
    assert(arreglo_agregar(&luces, luz_crear((vector_t){-2, 10, 2.5}, (color_t){.9, 0, 0}, true)));
    assert(arreglo_agregar(&luces, luz_crear((vector_t){2, 10, 2.5}, (color_t){0, .9, 0}, true)));
    assert(arreglo_agregar(&luces, luz_crear((vector_t){0, 10, 5}, (color_t){0, 0, .9}, true)));

    assert(luces.n == 4);
    for(size_t i = 0; i < luces.n; i++)
        assert(luces.v[i] != NULL);

    assert(arreglo_agregar(&esferas, esfera_crear((vector_t){0, 1, 2.4}, .3, (color_t){1, 1, 1}, 1, 1)));
    assert(arreglo_agregar(&esferas, esfera_crear((vector_t){0, -.4, 3}, 1, (color_t){1, 1, 1}, 1, 1)));

    assert(arreglo_agregar(&esferas, esfera_crear((vector_t){-2, -.6, 3}, .3, (color_t){1, 0, 0}, 1, .8)));
    assert(arreglo_agregar(&esferas, esfera_crear((vector_t){-1.73, -.6, 2}, .3, (color_t){1, 1, 0}, 1, 1)));
    assert(arreglo_agregar(&esferas, esfera_crear((vector_t){-1, -.6, 1.26}, .3, (color_t){0, 1, 0}, 1, 1)));
    assert(arreglo_agregar(&esferas, esfera_crear((vector_t){0, -.6, 1}, .3, (color_t){1, 1, 1}, 1, 1)));
    assert(arreglo_agregar(&esferas, esfera_crear((vector_t){1, -.6, 1.26}, .3, (color_t){0, 1, 1}, 1, 1)));
    assert(arreglo_agregar(&esferas, esfera_crear((vector_t){1.73, -.6, 2}, .3, (color_t){0, 0, 1}, 1, 1)));
    assert(arreglo_agregar(&esferas, esfera_crear((vector_t){2, -.6, 3}, .3, (color_t){1, 0, 1}, 1, 1)));

    assert(arreglo_agregar(&esferas, esfera_crear((vector_t){-3, 2.5, 4.3}, .3, (color_t){1, 1, 1}, 1, 0)));
    assert(arreglo_agregar(&esferas, esfera_crear((vector_t){-2, 2.5, 4.3}, .3, (color_t){1, 1, 1}, 1, .16)));
    assert(arreglo_agregar(&esferas, esfera_crear((vector_t){-1, 2.5, 4.3}, .3, (color_t){1, 1, 1}, 1, .33)));
    assert(arreglo_agregar(&esferas, esfera_crear((vector_t){0, 2.5, 4.3}, .3, (color_t){1, 1, 1}, 1, .5)));
    assert(arreglo_agregar(&esferas, esfera_crear((vector_t){1, 2.5, 4.3}, .3, (color_t){1, 1, 1}, 1, .66)));
    assert(arreglo_agregar(&esferas, esfera_crear((vector_t){2, 2.5, 4.3}, .3, (color_t){1, 1, 1}, 1, .83)));
    assert(arreglo_agregar(&esferas, esfera_crear((vector_t){3, 2.5, 4.3}, .3, (color_t){1, 1, 1}, 1, 1)));

    assert(arreglo_agregar(&esferas, esfera_crear((vector_t){-3, 1.5, 4}, .3, (color_t){1, 1, 1}, 0, 1)));
    assert(arreglo_agregar(&esferas, esfera_crear((vector_t){-2, 1.5, 4}, .3, (color_t){1, 1, 1}, .16, 1)));
    assert(arreglo_agregar(&esferas, esfera_crear((vector_t){-1, 1.5, 4}, .3, (color_t){1, 1, 1}, .33, 1)));
    assert(arreglo_agregar(&esferas, esfera_crear((vector_t){0, 1.5, 4}, .3, (color_t){1, 1, 1}, .5, 1)));
    assert(arreglo_agregar(&esferas, esfera_crear((vector_t){1, 1.5, 4}, .3, (color_t){1, 1, 1}, .66, 1)));
    assert(arreglo_agregar(&esferas, esfera_crear((vector_t){2, 1.5, 4}, .3, (color_t){1, 1, 1}, .83, 1)));
    assert(arreglo_agregar(&esferas, esfera_crear((vector_t){3, 1.5, 4}, .3, (color_t){1, 1, 1}, 1, 1)));

    assert(esferas.n == 23);
    for(size_t i = 0; i < esferas.n; i++)
        assert(esferas.v[i] != NULL);


    printf("P3\n");
    printf("%d %d\n", ANCHO, ALTO);
    printf("255\n");

    float vz = ANCHO / 2 / tan(FOV/ 2 * PI / 180);

    for(int vy = ALTO / 2; vy > - ALTO / 2; vy--)
        for(int vx = - ANCHO / 2; vx < ANCHO / 2; vx++) {
            color_imprimir(computar_intensidad(&esferas, &luces, ambiente, (vector_t){0, 0, 0}, vector_normalizar((vector_t){vx, vy, vz})));
            putchar('\n');
        }


    for(size_t i = 0; i < esferas.n; i++)
        esfera_destruir(esferas.v[i]);
    free(esferas.v);

    for(size_t i = 0; i < luces.n; i++)
        luz_destruir(luces.v[i]);
    free(luces.v);

    return 0;
}

Validación

La imagen generada por la cátedra con los mismos parámetros es la siguiente

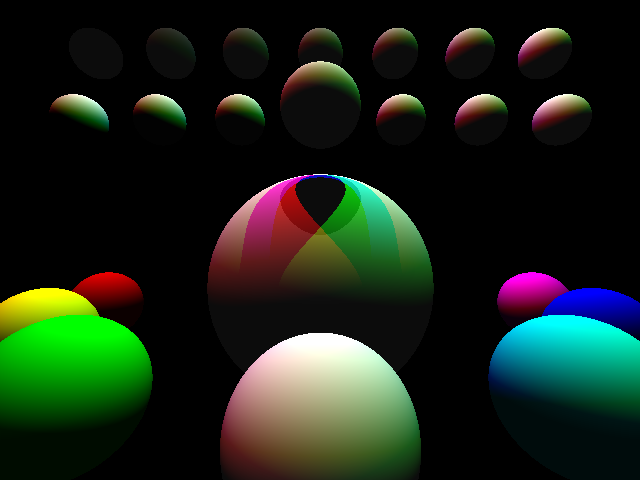
validar que la salida generada sea consistente con respecto a esta imagen de referencia.

Entrega

Deberá entregarse:

1. El código fuente del programa desarrollado,

2. la imagen generada o la captura correspondiente en formato JPG o PNG.

El programa debe:

1. Compilar correctamente con los flags:

   -Wall -Werror -std=c99 -pedantic
   

2. pasar Valgrind correctamente,

3. validar la imagen esperada.

La entrega se realiza a través del sistema de entregas.

El ejercicio es de entrega individual.