Trabajo Práctico 1

Fecha de entrega: Domingo 26 de diciembre

Introducción

Modelo completo de Phong

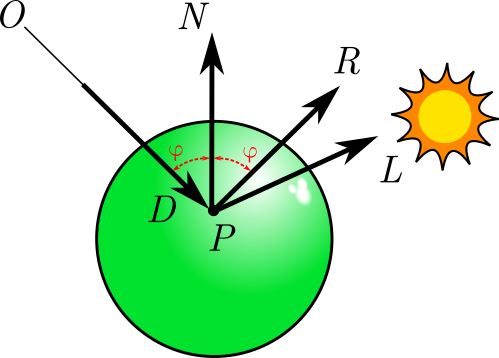
El modelo de Phong tiene tres componentes: ambiental, difusa y especular. Mientras que las dos primeras componentes dependen sólo de la posición de los objetos de la escena, la componente especular depende del punto de vista del observador. Esta componente lo que posee son los reflejos que se reciben desde las fuentes de luz.

Cuando se mira un objeto con dirección \(\hat D\) ese rayo rebota en la superficie simétricamente a la normal \(\hat N\) con dirección \(\hat R\). Puede computarse esta dirección como:

\[\hat R = \hat D - 2 \hat N (\hat D \cdot \hat N).\]

La componente especular estará dada por el ángulo entre \(\hat R\) y \(\hat L\), escalada de forma que esta componente tenga peso sólo cuando ambas direcciones sean muy colineares.

Sumando este término a la ecuación del color recibido en un punto obtenemos:

\[\vec C = \vec I_a k_a + \sum_{\forall i} \vec I_i \delta_{si} [k_d (\hat L_i \cdot \hat N) + k_s (\hat L_i \cdot \hat R)^\alpha],\]

donde \(k_s\) es el coeficiente de especular y \(\alpha\) es una constante que controla qué tan focalizado está el reflejo. En este trabajo tomaremos \(\alpha = 10\).

Como en trabajos anteriores, el coeficiente \(\delta_{si}\) indica si hay visibilidad o no desde el punto \(\vec P\) a la fuente de luz i-ésima. Ahora bien, notar que ambos términos entre los corchetes tienen un producto interno, el signo del producto del primer término indica que la luz está contraria a la normal mientras que en el segundo indica que está contraria al reflejo. Tanto en el caso difuso como en el caso especular si el producto interno respectivo diera negativo debe anularse ese y sólo ese término. (Es decir, no está bien considerar el signo del producto como parte del \(\delta_{si}\) dado que ahora hay dos términos con productos independientes entre sí.)

Paso recursivo

Si bien con el añadido anterior completamos el modelo de Phong podemos aprovechar esta base para mejorar el modelo. En la ecuación que construímos hasta el momento el color del material depende sólo de sí mismo y de las fuentes de luz incidentes. En la realidad los materiales también dependen de su entorno, es decir, los objetos y no sólo las luces que haya alrededor modificarán su color. Este fenómeno ocurre debido a que los fotones que parten de las fuentes de luz rebotan muchas veces en las diferentes superficies antes de incidir en la superficie de un objeto particular y finalmente llegar al ojo del observador.

En nuestro modelo en vez de simular la marcha de los fotones desde las fuentes de luz hacia el observador, recorremos el camino inverso: La marcha de rayos desde el observador hacia los objetos. Ahora bien, en la vida real cuando un rayo incide sobre un objeto, generalmente el mismo no muere ahí sino que rebota en el mismo y sigue rebotando infinidad de veces (si el ambiente fuera un espacio cerrado).

Para modelar este comportamiento agregaremos un paso recursivo a nuestro modelo. Cuando se computa la intensidad desde un origen y una dirección \(\mathrm{intensidad}(\vec O, \hat D)\) si esa dirección incide sobre un objeto entonces obtendremos un punto \(\vec P\) de intersección sobre su superficie. A partir de la normal \(\hat N\) en ese punto podemos computar el rayo reflejado \(\hat R\). Entonces, la información faltante sobre el entorno podrá computarse llamando a \(\mathrm{intensidad}(\vec P, \hat R)\). Este cómputo recursivo permitirá incorporar la información proveniente de los objetos del entorno.

Finalmente el cómputo del color total será adicionando:

\[\vec C' = \vec C + k_r \mathrm{intensidad}(\vec P, \hat R),\]

donde \(k_r\) es el coeficiente de reflexión.

Un par de observaciones importantes:

• La recursión sólo tendrá sentido computarla si es que:

  1. Hay intersección entre el rayo \(\vec O + t \hat D\) y algún objeto. En caso contrario se devolverá el color de fondo, como siempre.

  2. El coeficiente \(k_r > 0\), no tiene sentido computar esto si el objeto absorbe completamente el rayo.

• El punto \(P\) computado por las funciones de distancia estará justo sobre la superficie del objeto. Para evitar que por errores numéricos la llamada recursiva se choque contra el mismo objeto desplazar el punto a \(\vec P' = \vec P + \varepsilon \hat R\), donde \(\varepsilon\) puede ser un número muy pequeño, por ejemplo \(10^{-6}\).

• En la vida real los rayos rebotarán incontables veces, en nuestra implementación limitaremos la recursividad a un número determinado de pasos.

Objetos

De momento desarrollamos un único objeto que fue la esfera, en este trabajo desarrollaremos un par de objetos más. Al igual que con la esfera el objetivo para cualquier objeto será:

1. Encontrar la distancia \(t\) desde \(\vec O\) según la dirección \(\hat D\), si es que hubiera intersección.

2. Encontrar el punto \(\vec P = \vec O + t \hat D\).

3. Encontrar la normal \(\hat N\) en el punto \(\vec P\).

Planos

Un plano puede definirse a partir de una normal \(\hat N_p\) y un punto \(\vec P_p\).

Si eliminamos el caso particular de que la dirección coincida justo con el plano habrá siempre intersección a menos que la normal del plano sea ortogonal a la dirección del rayo, es decir siempre y cuando \(\hat D \cdot \hat N_p \neq 0\).

La distancia será

\[t = \frac{(\vec P_p - \vec O) \cdot \hat N_p}{\hat D \cdot \hat N_p},\]

donde la misma tiene que ser positiva para ser válida.

La normal en cualquier punto siempre será \(\hat N = \hat N_p\).

Triángulos

Un triángulo se puede definir por tres puntos \((\vec P^0_t, \vec P^1_t, \vec P^2_t)\).

Esos tres puntos generan dos lados:

\[\begin{split}\vec E^1_t = \vec P^1_t - \vec P^0_t,\\ \vec E^2_t = \vec P^2_t - \vec P^0_t.\end{split}\]

Notar que la dirección de la normal del triángulo estará dada por \(\vec N_t = \vec E^1_t \times \vec E^2_t\) (para que sea un versor habrá que normalizarla).

Un punto está dentro de un triángulo si tiene forma

\[\vec P = \vec P^0_t + u \vec E^1_t + v \vec E^2_t,\quad u \geq 0, v \geq 0, u + v < 1.\]

Podemos plantear el algoritmo de Möller-Trumbore para determinar si hay intersección. Computamos:

\[\begin{split}\vec h = \hat D \times \vec E^2_t,\\ a = \vec E^1_t \cdot \vec h.\end{split}\]

Si \(|a| < \varepsilon\) estamos ante un rayo paralelo al triángulo y no hay intersección.

Ahora podemos calcular:

\[\begin{split}\vec s = \vec O - \vec P^0_t,\\ u = \frac{\vec s \cdot \vec h}{a},\end{split}\]

donde sabemos que si \(u\) llegara a ser menor que 0 o mayor que 1 entonces no hay intersección.

Luego computamos:

\[\begin{split}\vec q = \vec s \times \vec E^1_t,\\ v = \frac{\hat D \cdot \vec q}{a},\end{split}\]

donde ahora sabemos que si \(v\) llegara a ser negativo o \(u + v > 1\) entonces no hay intersección.

Ahora sabemos que hay intersección, pero todavía no sabemos si es por delante o por detrás, debemos computar:

\[t = \frac{\vec E^2_t \cdot \vec q}{a},\]

y verificar que sea positivo.

La normal será la del triángulo.

Mallas

Es posible construir una malla como un arreglo de triángulos, donde la distancia estará dada por la intersección más cercana entre el rayo y todos los triángulos de la misma y la normal será la de ese triángulo.

El formato STL

El formato STL (Standard Triangle Language) es un formato muy sencillo para describir mallas.

El formato es un formato binario en little-endian.

Consiste en:

1. Un encabezado de 80 bytes (que puede ser descartado).

2. Un uint32_t que representa la cantidad de triángulos en el archivo.

3. Para cada uno de los triángulos:

   1. La normal \(\hat N_t\) representada como 3 float (un float tiene siempre 32 bits, acorde al estándar IEEE-754),

   2. El punto \(\vec P^0_t\) como 3 float,

   3. El punto \(\vec P^1_t\) como 3 float,

   4. El punto \(\vec P^2_t\) como 3 float,

   5. Dos bytes más (que representan un uint16_t que puede ser descartado).

Trabajo

Alcances

Mediante el presente TP se busca que el estudiante adquiera y aplique conocimientos sobre los siguientes temas:

• Encapsulamiento en TDAs,

• Punteros a funciones,

• Tablas de búsqueda,

• Archivos,

• Modularización,

• Técnicas de abstracción,

además de los temas ya evaluados en trabajos anteriores.

Nota

Este trabajo es un trabajo integrador de final de cursada. En el mismo se van a aplicar todos los temas aprendidos y además se va a evaluar el diseño de la aplicación.

Es imprescindible entender los temas de TDA y modularización antes de empezar con el trabajo.

Es imprescindible diseñar el trabajo como etapa previa a la implementación.

Cualquier abordaje que pretenda empezar a codificar sin haber ordenado el trabajo primero está condenado a fracasar contra la complejidad del problema.

Especificación

arreglo_t

Completar y encapsular el TDA arreglo ya desarrollado para el EJ2 para que el mismo sea completamente funcional (por ejemplo dotándolo de un constructor, un destructor que pueda liberar sus elementos, setters para lo que haga falta, etc.).

Objetos

Deben crearse TDAs para las esferas, los planos, los triángulos y las mallas.

Cada uno de estos tipos sólo guardará la información geométrica del objeto y resolverá las operaciones específicas de evaluación de distancias y normales.

Los triángulos deberán contener su normal, esto es para hacer más livianas las operaciones y para no depender del orden de definición de sus puntos.

Las mallas deberán poder ser creadas en base a un archivo (o su ruta) STL, deben ser respetadas las normales dadas por el archivo.

objeto_t

Debe crearse un TDA objeto_t el cual represente a un objeto de la escena. El mismo contendrá la información sobre el material, esto es tanto el color del objeto como sus coeficientes \(k_a, k_d, k_s, k_r\) y además tendrá una referencia a su geometría que será una esfera, plano, triángulo o malla.

El TDA tiene que proveer una primitiva

float objeto_distancia(const objeto_t *objeto, vector_t o, vector_t d, vector_t *punto, vector_t *normal);

que resuelva la llamada correspondiente para su geometría.

El destructor del TDA tiene que ser capaz de destruir la geometría que contiene.

La decisión de cómo invocar a la función de distancia o al destructor correspondiente no puede tomarse ni con estructuras condicionales sino que debe ser resuelta obligatoriamente mediante el uso de tablas de búsqueda.

Cómputo de la intensidad

Implementar la función

color_t computar_intensidad(int profundidad, const arreglo_t *objetos, const arreglo_t *luces, color_t ambiente, vector_t o, vector_t d);

que compute la intensidad para la escena y los parámetros dados. La variable profundidad indica cuántas veces debe computarse el cómputo de la reflexión recursiva. Si profundidad fuera cero esta función computará la escena sin reflexiones (como en el EJ3).

Aplicación

Se debe desarrollar un programa que se ejecute como

$ ./20212_tp1 [ancho] [alto] [profundidad] [nombrearchivo]

que genere sobre nombrearchivo una escena con las dimensiones y la profundidad de reflexiones dadas en formato PPM o BMP según corresponda.

La escena a dibujar queda a criterio completo del alumno, debiendo tener al menos una esfera, un plano, un triángulo y una malla STL y debiendo tener al menos una luz puntual y una no-puntual.

Siendo que el objetivo de la aplicación es dibujar una única escena no hay ningún requisito de elegancia en el código que genere la misma. Probablemente la misma termine siendo una sucesión de llamadas a primitivas de objetos con parámetros hardcodeados y no hay ningún problema en que así sea.

Tomar en cuenta que tanto la estructura de mallas como las operaciones sobre triángulos no son para nada eficientes. Esto va a limitar bastante la cantidad de objetos que se pueden poner en una escena, dado que el tiempo de cómputo va a crecer considerablemente conforme se agreguen más elementos. El tiemo siempre va a depender linealmente del producto ancho x alto y de la profundidad. Durante etapas de desarrollo usar tamaños pequeños, poca o nula profundidad, anular partes de la escena ya probadas o fuentes de luz. No llevar los parámetros al máximo hasta que se sepa que la escena va a funcionar bien.

Todo lo no especificado en este enunciado queda a criterio del alumno, pudiéndose agregar funcionalidades adicionales no contempladas siempre y cuando se implementen las pedidas.

Entrega

Requisitos

Los únicos requisitos son que el programa resuelva correctamente la funcionalidad pedida y que lo haga utilizando TDAs con un diseño planificado a conciencia. Si hacés eso nada puede salir mal.

Entregables

Deberá entregarse:

1. El código fuente del trabajo debidamente documentado.

2. El archivo Makefile para compilar el proyecto.

3. Una imagen con la escena desarrollada (en PNG o JPEG).

Nota

El programa debe:

• estar programado en C,

• estar completo,

• compilar...

• sin errores...

• sin warnings,

• correr...

• sin romperse...

• sin fugar memoria...

• resolviendo el problema pedido...

Trabajos que no cumplan con lo anterior no serán corregidos.

La entrega se realiza a través del sistema de entregas.

El ejercicio es grupal permitiéndose grupos de hasta 2 integrantes.

Si elegís hacer el trabajo en grupo te pedimos que nos avises o por mail o por Discord quién es tu compañero de grupo así lo cargamos en el sistema de entregas. (Si el grupo sufriera alteraciones avisanos también.)