Ejercicio obligatorio 2
Fecha de entrega: Viernes 22 de abril
Introducción
Polilíneas
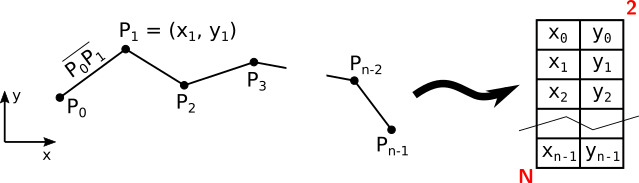
Una polilínea es una sucesión de segmentos de rectas en \(\mathbb R^2\) y puede ser construída a partir de una sucesión de puntos. Una polilínea de \(n - 1\) segmentos se construye a partir de \(n\) puntos.
En el lenguaje de programación C podemos representar este vector de puntos
utilizando una matriz float [N][2] como se muestra en el siguiente
esquema:
Distancia de punto a segmento de recta
Para determinar la distancia de un punto \(\vec P = (p_x, p_y)\) a un segmento de recta \(\overline{AB}\) dados por dos puntos \(\vec A = (a_x, a_y)\) y \(\vec B = (b_x, b_y)\), y asumiendo que la longitud de \(\overline{AB}\) es distinta de cero, puede computarse:
Si el parámetro \(\alpha \leq 0\) entonces el punto del segmento más cercano a \(\vec P\) es el punto \(\vec A\), si \(\alpha \geq 1\) el punto más cercano será \(\vec B\), y en el caso de que \(0 < \alpha < 1\) el punto más cercano estará dado por \(\vec A + \alpha \left( \vec B - \vec A \right)\).
Sabiendo cuál es el punto del segmento más cercano a \(\vec P\) se puede calcular esa distancia que será la distancia deseada.
Implementación
Traslación de puntos
Se pide implementar una función
void trasladar(float polilinea[][2], size_t n, float dx, float dy);
que, dado un vector polilinea con n puntos y el formato ya
descrito modifique cada una de sus componentes mediante la adición del par
(dx, dy).
Rotación de puntos
Se pide implementar una función
void rotar(float polilinea[][2], size_t n, double rad); que dada una
polilinea rote cada una de ella rad radianes con respecto al
origen de coordenadas.
Nota
Recordar que para rotar un par de coordenadas \((x, y)\) un ángulo \(\theta\) se debe realizar la operación:
\(\begin{bmatrix}x' \\y' \\\end{bmatrix} = \begin{bmatrix}\cos \theta & -\sin \theta \\\sin \theta & \cos \theta \\\end{bmatrix}\begin{bmatrix}x \\y \\\end{bmatrix}\).
La operación puede descomponerse como:
\(x' = x \cos \theta - y \sin \theta\),
\(y' = x \sin \theta + y \cos \theta\).
Distancia de punto a polilínea
Se pide implementar una función
double distancia_punto_a_polilinea(const float polilinea[][2], size_t n, float px, float py);
que dada una polilinea y un punto \(P\) de coordenadas (px, py)
calcule la distancia del punto a la polilínea.
Nota
Es recomendable construir funciones auxiliares para realizar este proceso.
Pruebas
Teniendo la poliínea \([(0, 1), (1, 3), (1, 5), (2, 5), (3, 4), (4, 4), (5, 3), (4, 2), (5, 1), (2, 0)]\) y además los puntos \([(0, 0), (0, 2), (6, 1), (2, 2), (1, 1), (1, 4), (5, 4), (-1, -3), (3, 3), (5, 3), (0, 7)]\) las distancias de cada uno de esos puntos a la polilínea respectivamente son:
1.0000000000
0.4472136322
1.0000000000
1.3416407687
0.8944271977
0.0000000000
0.7071067812
4.1231056256
1.0000000000
0.0000000000
2.2360679775
llamar a la función distancia_punto_a_polilinea() con TODOS estos valores,
validar que la distancia sea correcta (notar que la misma está expresada con
diez dígitos, no se espera un valor exacto a los 16 dígitos del double) e
imprimir un mensaje de error si alguno de los puntos no valida lo esperado.
Nota
Se estima que se pueden validar hasta 7 dígitos de estos valores, no más por acarreo de diferencias en las diferentes implementaciones.
Queda del lado del alumno probar las funciones trasladar() y rotar().
El main() del programa deberá correr los casos de prueba dados.
Entrega
Deberá entregarse el código fuente del programa desarrollado.
El programa debe compilar correctamente con los flags:
-Wall -Werror -std=c99 -pedantic
y validar los ejemplos dados.
La entrega se realiza a través del sistema de entregas.
El ejercicio es de entrega individual.