Trabajo Práctico 1

Fecha de entrega: Viernes 8 de Julio

Introducción

Objetivo

El objetivo del presente trabajo práctico es la implementación de una versión homenaje 40 años del juego Atari Gravitar utilizando gráficos de líneas en SDL2.

El trabajo consiste en la resolución de un problema mediante el diseño y uso de TDAs y en la reutilización de los tipos y funciones desarrollados a lo largo del curso en trabajos anteriores.

Alcances

Mediante el presente TP se busca que el estudiante adquiera y aplique conocimientos sobre los siguientes temas:

• Encapsulamiento en TDAs,

• Uso de listas enlazadas,

• Punteros a funciones,

• Archivos,

• Modularización,

• Técnicas de abstracción,

además de los temas ya evaluados en trabajos anteriores.

Nota

Este trabajo es un trabajo integrador de final de cursada. En el mismo se van a aplicar todos los temas aprendidos y además se va a evaluar el diseño de la aplicación.

Es imprescindible entender los temas de TDA y modularización antes de empezar con el trabajo.

Es imprescindible diseñar el trabajo como etapa previa a la implementación.

Cualquier abordaje que pretenda empezar a codificar sin haber ordenado el trabajo primero está condenado a fracasar contra la complejidad del problema.

Lógica del juego

El juego Gravitar es un juego de naves en el espacio. La nave tiene controles muy sencillos: Se puede rotar para un lado y para el otro, se puede acelerar en la dirección en la que apunta, puede disparar balas hacia adelante y puede prender su escudo. Cada instante en el que se acelera o se usa el escudo se consume combustible. La nave se mueve en el espacio sin rozamiento y la gravedad dependerá del estadío del juego.

El juego se inicia con una cantidad de combustible y con una cantidad de vidas. Cuando se acaba el combustible o las vidas el juego se pierde. El combustible se repone secuestrando tanques de combustible y las vidas se reponen a razón de una cada 10000 puntos obtenidos. Los puntos se obtienen de atacar a los enemigos.

Dentro del juego hay un par de pantallas diferentes:

Pantalla de selección:

El juego se inicia en la pantalla de selección. La nave está detenida en la base. En este nivel, la gravedad la ejerce la estrella, atrayendo la nave hacia sí. Si la nave colisiona con la estrella se pierde la vida recomenzando en la base. En la pantalla además hay planetas. Si se toca uno de los planetas se accede al nivel que este representa.

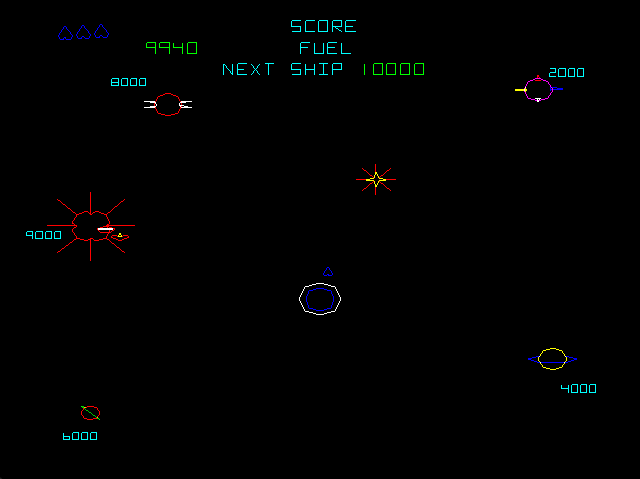
En la pantalla de selección si la nave intenta escaparse de la pantalla rebota otra vez hacia adentro.

Pantalla de planetas:

Cuando se accede a un planeta se navega por encima del mismo, el planeta ejerce gravedad hacia abajo. Si se colisiona con la superficie del planeta se pierde la vida.

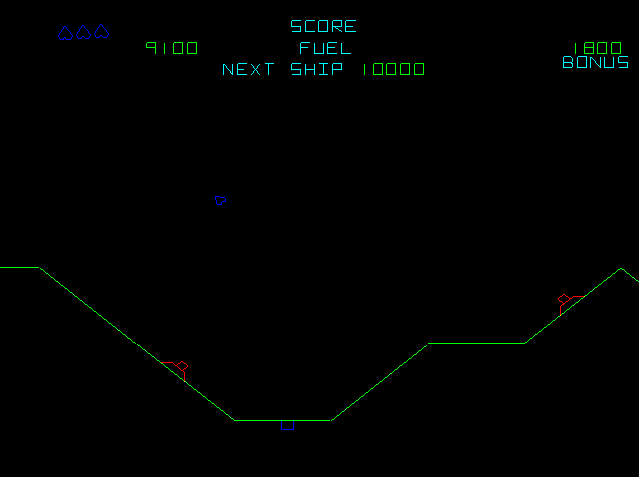
En el planeta hay tanques de combustible que pueden secuestrarse volando cerca de ellos y activando el escudo. También en el planeta hay torretas que disparan balas y a las que puede dispararse y destruirlas.

Hay dos tipos de planetas, los de superficie "infinita", la cual se repite cíclicamente en el sentido de las equis y los que están fijos. La imagen anterior se corresponde a un planeta infinito y la que sigue a continuación a un planeta fijo.

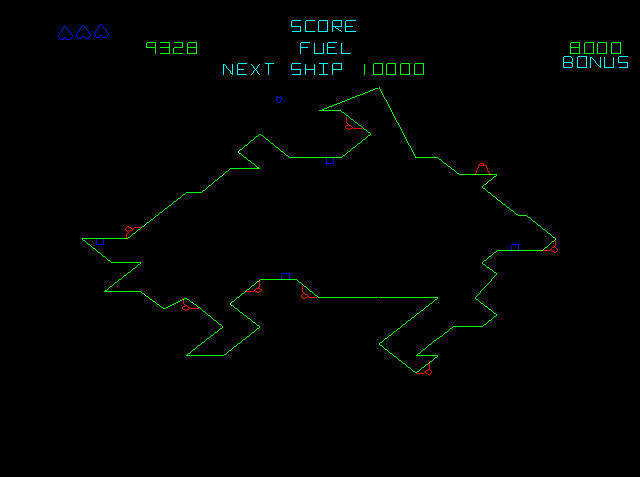
En los planetas infinitos la nave se acerca a la superficie y la puede recorrer, en los fijos el planeta queda estático y la nave se desplaza a su alrededor. Como se dijo antes, la gravedad es siempre hacia abajo, incluso si se está recorriendo un planeta por debajo.

En los planetas si la nave se aleja de la superficie (en los infinitos sólo puede hacerlo hacia arriba) y sale de la pantalla se vuelve a la pantalla de selección.

Hay planetas en los que hay un reactor. El reactor debe ser destruido por nuestra nave en menos de 25 segundos o el mismo explota y se pierde la vida.

Pantalla de duelo:

Cuando en la pantalla de selección una nave enemiga se acerca lo suficiente se entra a una pantalla en blanco, sin gravedad, donde se combate con esa nave. La misma no termina hasta que una de las dos naves sea destruida. En esta pantalla la nave rebota contra los bordes de la ventana.

En este trabajo no es parte de la consigna implementar esta pantalla ni tampoco implementar naves enemigas.

Especificación

Detalles

Nota

Se provee el archivo config.h con la especificación de todas las constantes que se mencionan.

Pantalla

En SDL2 el origen de coordenadas está arriba a la izquierda. Las equis crecen hacia la derecha, las yes hacia abajo.

En la física de nuestro juego el origen está abajo a la izquierda. Esta diferencia debe ser atendida al dibujar.

Física

El juego se ejecuta a la tasa de JUEGO_FPS cuadros por segundo, de donde se puede calcular inmediatamente el DT, que es la duración de cada cuadro.

La nave posee una posición y una velocidad. La velocidad puede ser afectada por la gravedad o también por el chorro que impulsa la nave. Cuando se activa el chorro de la nave el mismo genera una fuerza hacia adelante durante el tiempo que esté prendido.

Los disparos tienen una posición y una velocidad y no se ven afectados por la gravedad.

Límites de la pantalla

Como ya se dijo, hay distintos comportamientos de la pantalla según el tipo de nivel.

En los niveles donde la nave rebota se debe chequear si la posición de la nave es menor a 0 o mayor que la dimensión de la ventana. De ocurrir esto simplemente se invierte el valor de la velocidad correspondiente a ese eje.

En los planetas hay un par de consideraciones adicionales que se detallarán a continuación.

Queremos garantizar que la nave esté siempre dentro de un recuadro de la pantalla y que la cámara se desplace siguiendo a la nave cuando se escapa de él. Esto no afecta la física del juego. La física del juego se mantiene sin cambios, con su propio sistema de coordenadas en el que se hacen las operaciones.

Al respecto de la física, cada nivel tiene un determinado ancho en pixeles, dado por los límites de sus polilíneas. La nave debe mantenerse dentro de este límite. El efecto circular se obtiene restándole el ancho del nivel a la posición de la nave si la misma supera al ancho, o sumándoselo si la posición se hiciera negativa.

Al respecto del recuadro de nuestro mundo que veremos en la pantalla en el juego siempre el borde de abajo se corresponde con la altura cero y queremos que la nave esté dentro de un recuadro centrado en la pantalla. Definiremos dos cosas, un factor de escala, que va a hacer que todo se achique si la nave está lejos del suelo, para que entre en cuadro, y una coordenada de centro que será la que corresponde a la coordenada de equis que se ve en el centro de la pantalla.

Estos dos números pueden calcularse de la siguiente manera:

float escala = 1;
if(posicion_nave_y > VENTANA_ALTO * MARGEN_ALTURA)
    escala = VENTANA_ALTO * MARGEN_ALTURA / posicion_nave_y;
if(escala < ESCALA_MINIMA)
    escala = ESCALA_MINIMA;

if((posicion_nave_x - centro) * escala > VENTANA_ANCHO / 2 * MARGEN_ANCHO)
    centro = posicion_nave_x - VENTANA_ANCHO / 2 * MARGEN_ANCHO / escala;
else if((centro - posicion_nave_x) * escala > VENTANA_ANCHO / 2 * MARGEN_ANCHO)
    centro = posicion_nave_x + VENTANA_ANCHO / 2 * MARGEN_ANCHO / escala;

notar que la escala se calcula cada vez mientras que el centro es una variable que mantiene su valor, mientras la nave no se escape de los márgenes definidos el centro se mantiene estático.

Notar además que se establece una estala mínima, cuando se llegue a esa escala la pantalla no se achicará más y la nave podrá escaparse hacia arriba, terminando el nivel. La nave saldrá de la pantalla cuando posicion_nave_y > VENTANA_ALTO / ESCALA_MINIMA.

Teniendo la escala y el centro, cada coordenada (x, y) que quiera dibujarse en la pantalla tendrá que trasladarse en x en centro + VENTANA_ANCHO / 2 / escala y multiplicarse por escala. (Como ya se dijo, las yes están invertidas, se deja esa cuenta.)

Para que los objetos en la pantalla se vean infinitos al dibujarlos puede dibujarse una copia desplazada en -ancho y otra en ancho.

Puntajes

El juego se inicia con cero puntos y con 10000 unidades de combustible.

Si hubiera naves enemigas cada nave destruida suma 100 puntos.

Cada torreta destruida suma 250 puntos.

Cada nivel completado (destruidas todas las torretas) suma el puntaje del nivel.

Cada segundo completo de potencia consume 250 unidades de combustible.

Cada segundo completo de escudo consume 500 unidades de combustible.

Cada tanque de combustible capturado suma 3000 de combustible.

El juego inicia con 3 vidas, por cada 10000 puntos se gana una vida adicional.

Se tiene (y/o se debería completar)

• Funciones para computar velocidad y posición en base a aceleraciones del EJ1. Se deben usar para modificar la nave.

• El TDA polilinea_t. A la definición del EJ3 hay que agregarle un color, con su respectivo getter y setter (y verificar la lógica, por ejemplo al clonar).

  Integrar al TDA como primitivas las funciones ya desarrolladas en el EJ2 de distancia, rotación y traslación.

• En el EJ4 se trabajó sobre figuras, las mismas sólo se imprimieron pero nunca se almacenaron. Es necesario implementar el TDA figura, las figuras tienen los atributos ya documentados en el EJ4.

• Debe poder crearse un contenedor que tenga todas las figuras desde un archivo. El contenedor bien puede ser un arreglo dinámico (no hace falta un TDA vector, pero puede usarse) o una lista enlazada.

• Los tipos de figuras finales son: Icono, Nivel, Sprite, Planeta, Base, Combustible, Torreta, Reactor, en ese orden, numerados del 0 al 6. Completar el enumerativo del EJ4.

• Para escribir textos en la pantalla se proveyeron vectores de polilíneas (const float [][2]) que representan cada carácter. Los mismos deben ser indexados en una tabla de búsqueda que permita relacionar char con el vector correspondiente y con su número de puntos. Integrado en el TP debe programarse alguna función que permita dibujar una cadena de caracteres en determinada posición de la pantalla y con determinado color. Trabajar los caracteres como fueron dados en const float [][2], no construir polilineas, son innecesarias.

• Se tiene el TDA lista enlazada dado en clase, el mismo debe ser utilizado sin modificaciones.

Implementación

Un juego gráfico, una vez iniciado, consiste en un bucle principal que itera una vez por cada DT, es decir, a una tasa de tantos FPS por segundo. En cada iteración hay que hacer 3 cosas:

1. Verificar si el usuario presionó o soltó una tecla y modificar los estados correspondientes.

2. Computar la física para un DT adicional y luego verificar el estado de las reglas del juego.

3. Dibujar en la pantalla todos los objetos y textos que hagan falta.

Estos tres pasos se deben resolver todo el tiempo.

Siendo que el juego tiene diferentes etapas, las mismas deben ser implementadas de forma excluyentes entre sí. Se recomienda tener algún enumerativo que describa el estado actual y tomar decisiones en función de eso. Cuando ocurran los eventos que cambian el estado se deben ajustar las variables del juego correspondientes.

Dibujado

Los elementos del juego están asociados con figuras, las cuales están contenidas en el archivo de figuras desarrollado en el EJ4.

Todas estas figuras están descriptas a escala 1, en el origen de coordenadas y sin rotar.

Las figuras deben ser cargadas en memoria una única vez, y las mismas podrán ser identificadas sólo por su nombre y tipo (no puede asumirse un orden específico).

Cada vez que haya que dibujar un elemento del juego deberá buscarse la figura correspondiente a ese elemento. Puede ser conveniente que los TDAs puedan informar qué figura corresponde para su estado, por ejemplo, la nave puede informar si en ese momento debe ser dibujada con la figura "NAVE" o la figura "NAVE+CHORRO" según si está recibiendo potencia o no.

Cada figura posee una serie de polilíneas. Para dibujar la figura en la pantalla, en una posición específica y con una determinada rotación, para cada una de sus polilíneas deben clonarse, rotarse, trasladarse, luego dibujarse (de haber escala lo más conveniente es escalar al dibujar) y finalmente destruirse esa copia.

Notar que la operación de dibujado es algo que es independiente de los TDAs, los cómputos, los estados del juego, etc. Es una operación apenas de impresión que se realiza de forma independiente usando los datos del juego.

Trabajo

El enunciado de este trabajo será breve, no se introducirá ningún concepto nuevo. Ya tenemos implementado nuestro TDA polilinea_t y tenemos desarrollada parte de la lógica de lectura de figuras, también funciones para el manejo del motor físico, en los códigos ya dados se encuentra además la lógica de lectura de un archivo de niveles, y se encuentra provista por la cátedra la implementación del TDA lista enlazada.

El problema que se plantea en este trabajo deberá ser resuelto con las herrramientas ya adquiridas, extendiendo de forma consistente los TDAs ya planteados y diseñando los TDAs nuevos que hagan falta. Se evaluará además el correcto uso de los TDAs respetando la abstracción y el "modelo" de Alan-Bárbara.

TDAs

Aplicación

Se pide diseñar una aplicación que pueda ser ejecutada como:

$ ./gravitar

que permita jugar al juego Gravitar, con toda la lógica del problema y que sea capaz de informar al usuario de los eventos, su puntaje, sus vidas, combustible, etc.

Encapsulamiento

Se deben implementar TDAs donde se considere que es necesario.

Deben ser un TDA al menos: La nave, los disparos, las torretas, las figuras.

Los tres primeros representan objetos dinámicos del juego, tanto la nave como los disparos se desplazan, por lo que contienen variables sobre su física (posición, velocidad, dirección, etc.) y pueden tomar decisiones, como por ejemplo un disparo considerar que ya superó su tiempo máximo y debe destruirse o la torreta decidir si dispararle a la nave.

La nave es única, pero los disparos, las torretas, el combustible (sí, no está obligado a ser TDA pero es una entidad del juego), son múltiples por lo que deben ser almancenados en listas enlazadas.

En cada paso de tiempo estos objetos tienen que ser actualizados, donde la actualización consistirá, por ejemplo, en moverse un dt.

Para los objetos múltiples la idea será iterar las listas:

para cada elemento en lista:
    actualizar elemento;

También se usarán iteraciones de lista para verificar colisiones, descartar elementos, etc. Por ejemplo:

para cada disparo en lista_disparos:
    si distancia(disparo, nave) < RADIO:
        matar nave;
        eliminar disparo de la lista;

O:

para cada disparo en lista_disparos:
    si disparo_expiro():
        eliminar disparo de la lista;

Las iteraciones pueden hacerse tanto con el iterador externo como con las primitivas de filtrar.

Niveles

Los siguientes son los parámetros del juego:

Base:

La base utiliza la figura "BASE" y está en la coordenada (388, 218). La nave debe iniciar en esa posición.

Estrella:

La estrella utiliza la figura "ESTRELLA" y está en la coordenada (457, 364). La dirección de esta coordenada define la gravedad que recibe la nave. La estrella mata a la nave.

Planetas:

Nivel 1: Entrega 2000 puntos, utiliza la figura "PLANETA1", se ubica en las coordenadas (663, 473).

Nivel 2: 4000 puntos, "PLANETA2", (671, 145).

Nivel 3: 6000, "PLANETA3", (110, 79).

Nivel 4: 8000, "PLANETA4", (204, 455).

Nivel 5: 9000, "PLANETA5", (111, 307).

Niveles:

Nivel1: Utiliza la figura "NIVEL1NE", posee dos tanques de combustibles en (x, y, angulo -radianes-): (1064, 13, 0), (1685, 113, 0), posee dos torretas en (x, y, angulo): (916, 75, -0.66), (1425, 159, 0.66).

Nivel2: Utiliza la figura "NIVEL1SE", posee combustible en {(482, 94, 0), (1751, 247, 0)} y torretas en {(423, 195, -0.66), (806, 215, -0.33), (1254, 153, 0.66), (1587, 223, 2.23)}.

Nivel3: Utiliza la figura "NIVEL1SW", posee combustible en {(820, 46, 0), (1196, 68, 0), (1602, 46, 0)} y torretas en {(70, 46, 0), (506, 12, 0), (952, 12, 0), (1385, 12, 0), (757, 210, 3.14), (1161, 210, 3.14)}.

Nivel 4: Utiliza la figura "NIVEL1NW", posee combustible en {(188, 429, 0), (667, 600, 0), (1054, 404, 3.14), (574, 344, 3.14)} y torretas en {(257, 440, 0.66), (719, 674, 2.23), (985, 565, 0), (1125, 417, 3.8), (862, 163, 3.8), (626, 323, 2.23), (505, 331, 3.8), (378, 296, 2.23)}.

Nivel5: Utiliza la figura "NIVEL1R", tiene un reactor en coordenadas (815, 309, 0), el reactor debe eliminarse en menos de 25 segundos.

Notar que el juego recuerda los elementos eliminados en los diferentes planetas, por lo que es necesario que estos parámetros se vuelquen en estructuras indexables y actualizables durante el juego.

Alcance

El alcance inicial del juego es el especificado y una buena implementación del mismo es suficiente para alcanzar la máxima nota. La prioridad es resolver completa esta funcionalidad descrita para terminar con eso la materia.

Ahora bien, por simplificar el enunciado se dejaron afuera de la especificación muchos detalles del juego original que pueden ser implementados como puntos

Material

Implementaciones

Se cuenta con la implementación de lista enlazada mandada por correo el día 30/05.

Se proveen los archivos de caracteres, el binario con las figuras y un ejemplo de SDL2 en: archivos_20221_tp1.tar.gz

Valgrind

En el caso de una aplicación construída con SDL2 se hace complejo el uso de Valgrind porque esta biblioteca tiene desprolijidades en su implementación que hacen que Valgrind tire múltiples errores y estos errores a la tasa que marquen los FPS del juego. Por eso para poder testear con Valgrind sobre el código desarrollado tenemos que suprimir los errores que son relativos a SDL2.

Se provee el siguiente archivo de supresiones para Valgrind: suppressions_20221_tp1.supp

Con este archivo descargado Valgrind puede ser invocado como:

$ valgrind --suppressions=suppressions_20221_tp1.supp --leak-check=full ./gravitar

con lo que el programa se ejecutará suprimiendo los millones de erroes de SDL2.

Al haber errores y haberlos suprimido el reporte no será del todo satisfactorio, y va a haber memoria en el heap y elementos marcados como "still reachable". El siguiente es un reporte de ejemplo:

==27213== Memcheck, a memory error detector
==27213== Copyright (C) 2002-2017, and GNU GPL'd, by Julian Seward et al.
==27213== Using Valgrind-3.13.0 and LibVEX; rerun with -h for copyright info
==27213== Command: ./peggle peggle.bin
==27213==
==27213==
==27213== HEAP SUMMARY:
==27213==     in use at exit: 196,326 bytes in 1,058 blocks
==27213==   total heap usage: 32,817 allocs, 31,759 frees, 118,233,488 bytes allocated
==27213==
==27213== LEAK SUMMARY:
==27213==    definitely lost: 0 bytes in 0 blocks
==27213==    indirectly lost: 0 bytes in 0 blocks
==27213==      possibly lost: 0 bytes in 0 blocks
==27213==    still reachable: 2,037 bytes in 10 blocks
==27213==         suppressed: 194,289 bytes in 1,048 blocks
==27213== Reachable blocks (those to which a pointer was found) are not shown.
==27213== To see them, rerun with: --leak-check=full --show-leak-kinds=all
==27213==
==27213== For counts of detected and suppressed errors, rerun with: -v
==27213== ERROR SUMMARY: 0 errors from 0 contexts (suppressed: 1018824 from 25)

Notar que pese a que se señala más de un millón de errores, el reporte de pérdidas dice que no hay bloques ni definitiva, ni indirecta ni posiblemente perdidos. Además el reporte, pese a haber sido corrido con --leak-check=full no muestra ningún error en nuestro propio código.

Se busca que el reporte tenga estas características.

Ahora bien, prestar atención porque ignorar los errores de still reachable puede enmascarar errores como por ejemplo no haber llamado a fclose() entre otros.

Nota

Ejecutar con Valgrind implica a poner a un programa a analizar cada cosa que hace nuestro programa. Con un programa pesado en cantidad de operaciones como el nuestro, el programa va a andar muy lento.

La idea es correr con Valgrind como un chequeo a realizar, pero no todo el tiempo durante del desarrollo.

Para liberar la carga, sólo durante las corridas de Valgrind, se puede reducir el valor de JUEGO_FPS a un valor que lo haga más manejable. Esto va a romper la física del juego, pero al menos va a permitir testear más intensivamente la memoria.

Entrega

Requisitos

Los únicos requisitos son que el programa resuelva correctamente la funcionalidad pedida y que lo haga utilizando TDAs con un diseño planificado a conciencia. Si hacés eso nada puede salir mal.

Entregables

Deberá entregarse:

1. El código fuente del trabajo debidamente documentado.

2. El archivo Makefile para compilar el proyecto.

Nota

El programa debe:

• estar programado en C,

• estar completo,

• compilar...

• sin errores...

• sin warnings,

• correr...

• sin romperse...

• sin fugar memoria...

• resolviendo el problema pedido...

Trabajos que no cumplan con lo anterior no serán corregidos.

La entrega se realiza a través del sistema de entregas.

El ejercicio es grupal permitiéndose grupos de hasta 2 integrantes.

Si elegís hacer el trabajo en grupo te pedimos que nos avises o por mail o por Discord quién es tu compañero de grupo así lo cargamos en el sistema de entregas. (Si el grupo sufriera alteraciones avisanos también.)

Parte 2: Aclaraciones

Estos comentarios podrían agregarse al enunciado, pero para hacer más visible la identificación los pongo al final.

config.h

G:

Es la aceleración que recibe la nave en todo momento. En la pantalla de selección con dirección hacia la estrella, en la de planeta hacia abajo.

NAVE_ACELERACION:

Es la aceleración que impulsa a la nave cuando el chorro está prendido. Se aplica en el ángulo de la nave.

NAVE_ROTACION_PASO:

Cada instante que esté apretada la tecla de rotar esta será la cantidad de radianes que girará sobre su eje.

VENTANA_ANCHO, VENTANA_ALTO:

Dimensiones de la ventana.

MARGEN_ALTURA, MARGEN_ANCHO: Proporciones límites de la plantalla

dentro de los cuales tiene que estar la nave en planetas infinitos.

ESCALA_MINIMA: Menor relación de escala antes de que se deje escapar a la

nave en planetas infinitos.

Planetas no infinitos

En los planetas infinitos la escala y el centro dependen de la posición de la nave y se dieron las fórmulas para calcularlas.

En los planetas no infinitos el planeta tiene que quedar dibujado centrado en la pantalla. Por lo que tanto la escala como el centro dependen del planeta.

Hay planetas como el NIVEL1R que ocupan el ancho completo de la pantalla mientras que otros como el NIVEL1NW que tienen que poder ser navegados alrededor. ¿Cómo se diferencian entre sí?, por la coordenada mínima en equis. El mínimo de equis marca el margen que hay que dejar hacia los lados. Es decir, si el mínimo en equis vale 0 entonces no hay margen, si el mínimo vale 300 entonces ese margen tiene que ser replicado hacia derecha también (por lo que el ancho real será ancho + margen).

Las cuentas para computar la escala y el centro son:

escala = VENTANA_ALTO * 1.0 / planeta_alto;
if(VENTANA_ANCHO * 1.0 / (planeta_ancho + planeta_x_min) < escala)
    escala = VENTANA_ANCHO * 1.0 / (planeta_ancho + planeta_x_min);
centro = (planeta_ancho + planeta_x_min) / 2;

Notar que teniendo definido centro y escala se pueden usar las mismas funciones de graficación que para los niveles infinitos. (Y si ahí se triplicaran los objetos, puede mantenerse eso haciéndolo cada planeta_ancho + planeta_x_min, que van a quedar siempre fuera de pantalla.)

Funcionamiento

Para poder ver el comportamiento tanto de la física, tiempos, movimiento de pantalla, niveles, etc. se grabó este video (con vidas infinitas) que muestra diferentes situaciones y pasa por todos los niveles:

Puede descargarse la grabación original (sin la compresión de YouTube) de acá: https://drive.google.com/file/d/1DMP2ft_lU2TWzOiE8_qgwWj42Xb6JcFc/view?usp=sharing