Ejercicio obligatorio 1

Fecha de entrega: Lunes 12 de septiembre

Nota

Nunca es buena idea empezar por un ejercicio integrador antes de tener practicados los temas que el trabajo integra.

Se sugiere antes de desarrollar este trabajo resolver, al menos, los siguientes ejercicios de la guía de Introducción al lenguaje C:

• Ejercicio 1 (interés compuesto).

• Ejercicio 5 (norma de un vector en \(\mathbb R^3\)).

• Ejercicio 13 (tabla del 7).

• Ejercicio 14 (tabla de multiplicar).

Introducción

Netpbm

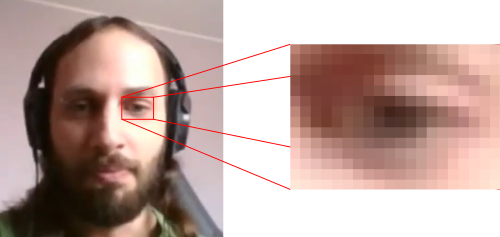
Cuando representamos una imagen de forma digital lo que hacemos es generar una grilla regular de puntos, cada uno de ellos llamado píxel (picture element). El pixel es la mínima unidad y se define por el color de ese punto de la imagen. Al mirar la imagen desde lejos esta grilla discreta se percibe como un contínuo de colores.

Netpbm es un paquete de utilidades para imágenes que describe varios formatos para guardar gráficos que se destacan por su simplicidad. Los tres formatos más importantes que define son PBM (portable bit map) para gráficos monocromos, PGM (portable gray map) para gráficos en escalas de grises y PPM (portable pixel map). Si bien todos los formatos se parecen, describiremos el formato PGM, que es el que utilizaremos en este trabajo.

La variante ASCII del formato PGM consiste en un encabezado que especifica el tipo de archivo (la secuencia "P2"), el tamaño de la imagen y el máximo valor de gris y, a continuación, los pixeles de la imagen que varían entre cero y el valor que se haya puesto como máximo. Cero es negro, el máximo es blanco y los valores intermedio serán grises.

Versión corta: P2 + ancho + alto + maximo + pixeles

El separador entre cada una de estas cosas es un carácter blanco, donde se considera blanco a un espacio, pero también a una tabulación, nueva línea, etc.

Hay una restricción adicional y es que ninguna línea puede ser mayor a 70 caracteres, por lo que por simplificar podemos separar por nuevas líneas.

Por ejemplo el siguiente archivo:

P2
20 7
15
0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0
0  3  3  3  3  0  0  7  7  7  7  0  0 11 11  0  0 15 15  0
0  3  0  0  3  0  0  7  0  0  0  0  0  0 11  0  0  0 15  0
0  3  3  3  3  0  0  7  7  7  7  0  0  0 11  0  0  0 15  0
0  0  0  0  3  0  0  0  0  0  7  0  0  0 11  0  0  0 15  0
0  3  3  3  3  0  0  7  7  7  7  0  0  0 11  0  0  0 15  0
0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0

genera la imagen (ampliándola varias veces):

Esto es una imagen PGM de 20 pixeles de ancho, por 7 de alto, donde hay 16 valores de gris definidos entre el 0 y el 15. Al ser de 20x7 la imagen tiene 140 píxeles.

Los píxeles en una imagen se definen siempre de izquierda a derecha y de arriba a abajo. Es decir, el origen de coordenadas está arriba a la izquierda y el eje \(x\) apunta hacia la derecha mientras que el eje \(y\) apunta hacia abajo.

Distancia entre dos puntos

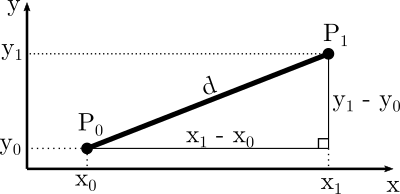
Si tenemos dos puntos \(P_0, P_1 \in \mathbb R^2\) de coordenadas \(P_0 = (x_0, y_0)\) y \(P_1 = (x_1, y_1)\) sabemos que la distancia euclídea \(d\) entre esos dos puntos estará dada por

\[d(P_0, P_1) = \sqrt{ (x_0 - x_1)^2 + (y_0 - y_1)^2}.\]

Senos

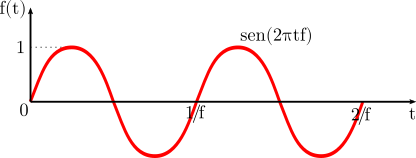
Podemos definir un seno en función de su frecuencia \(f\) como:

\[f(t) = sin(2\pi f t).\]

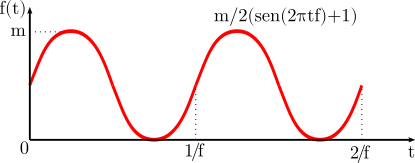
Sabemos que la función seno da valores entre \((-1, 1)\). Si quisiéramos generar un seno entre cualquier valor \((0, m)\) alcanzaría con transformar linealmente estos valores según

\[f(t) = \frac m2 (\sin(2\pi f t) + 1).\]

Trabajo

Distancia

Se pide implementar la función double distancia(float x0, float y0, float x1, float y1); que calcule la distancia entre los dos puntos dados por (x0, y0) y (x1, y1).

Seno

Se pide implementar la función int seno_escalado(double t, float f, int max) que devuelva el valor del seno de frecuencia f en el instante t escalado de tal manera que su resultado esté entre (0, max).

Gráfico

Dadas las siguientes definiciones:

#define ANCHO 640
#define ALTO 480
#define MAXIMO 255

#define X0 (ANCHO / 2)
#define Y0 (ALTO / 2)

#define FRECUENCIA 0.02

Se pide implementar un programa que genere una imagen PGM de ANCHO por ALTO, con un máximo de gris de MAXIMO donde el valor de cada pixel de la imagen, de coordenadas \((x, y)\), se calcule como el seno de la distancia del pixel al (X0, Y0) a la FRENCUENCIA dada.

Es decir, para cada pixel de la imagen se tendrá:

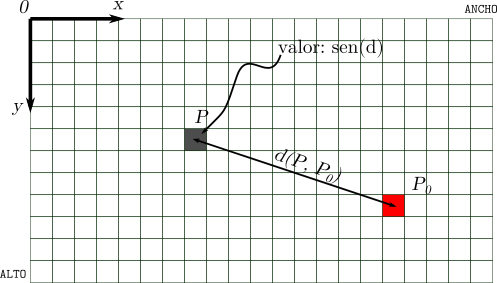
Graficación

Se pide abrir la imagen generada con un visor de imágenes de su preferencia (gimp, eog, etc.).

Convertir la imagen a PNG o JPG o realizar una captura de pantalla donde se vea la imagen abierta.

Validación

La imagen generada por la cátedra con los mismos parámetros es la siguiente

validar que la salida generada sea consistente con respecto a esta imagen de referencia.

Entrega

Deberá entregarse:

1. El código fuente del programa desarrollado.

2. La imagen generada o la captura correspondiente en formato JPG o PNG.

La entrega se realiza a través del sistema de entregas.

El ejercicio es de entrega individual.