Trabajo Práctico 1

Fecha de entrega: Domingo 4 de diciembre

Introducción

Objetivo

El objetivo del presente trabajo práctico es la implementación de una reversión del juego de arcade Hang-On de Sega, del año 1985 aplicando la biblioteca de imágenes desarrollada durante el cuatrimestre en conjunto con la biblioteca SDL2.

El trabajo consiste en la resolución de un problema mediante el diseño y uso de TDAs y en la reutilización de los tipos y funciones desarrollados a lo largo del curso en trabajos anteriores.

Alcances

Mediante el presente TP se busca que el estudiante adquiera y aplique conocimientos sobre los siguientes temas:

• Encapsulamiento en TDAs,

• Contenedores y tablas de búsqueda,

• Punteros a funciones,

• Archivos,

• Modularización,

• Técnicas de abstracción,

además de los temas ya evaluados en trabajos anteriores.

Nota

Este trabajo es un trabajo integrador de final de cursada. En el mismo se van a aplicar todos los temas aprendidos y además se va a evaluar el diseño de la aplicación.

Es imprescindible entender los temas de TDA y modularización antes de empezar con el trabajo.

Es imprescindible diseñar el trabajo como etapa previa a la implementación.

Cualquier abordaje que pretenda empezar a codificar sin haber ordenado el trabajo primero está condenado a fracasar contra la complejidad del problema.

Estructura y lógica del juego

El juego Hang-On es un juego de motos de arcade desarrollado por Yu Suzuki en el año 1985 para la compañía Sega. El mismo contaba con un hardware específicamente desarrollado para tal fin: la arquitectura Sega System 16, y el primero en utilizarla.

La gran innovación del juego consistió en lograr una emulación 3D convincente teniendo una lógica interna puramente 2D. Para esto la arquitectura contaba con una serie de chips dedicados a la resolución de diferentes problemas de computación gráfica en 2D los cuales fueron emulados en software en las instancias previas de ejercicios obligatorios de esta materia. El fuerte de la arquitectura System 16 era la posibilidad de escalar y posicionar imágenes sobre cualquier posición de la pantalla en tiempo real y para eso tenía 5 chips dedicados a tal efecto.

La pantalla del juego tenía una resolución de 320x224 pixeles y respondía al siguiente esquema:

y consiste en una composición de imágenes que, en el juego real, provenían de diferentes componentes de hardware. Mencionaremos cada una de ellas:

Fondo:

El fondo es sobre lo que se componen el resto de las gráficas. Consiste en el color del cielo, el color del terreno y un gradiente de colores sobre el terreno cerca del horizonte. La generación del mismo ya fue provista en el main() del EJ4.

Fondo1 y fondo2:

Para dar la sensación de profundidad el juego imprimía dos imágenes de fondo sobre el horizonte usando la técnica multiplano. La ubicación de las imágenes depende del giro que se ha dado sobre la pista y desplazándose la segunda imagen más lento que la primera imprime una sensación de lejanía y profundidad. Estas imágenes se generaban con chips de Tilemap Generator que imprimían un mosaico de teselas en una posición específica y se corresponden con los mosaicos desarrollados en el EJ4.

Ruta:

Para el dibujo de la ruta había un chip específico. Dentro de una ROM se encontraba almacenada la representación de la ruta con perspectiva central de la ruta recta, y el efecto de perspectiva y de tridimensionalidad ante las curvas se lograba dibujando desplazadas cada una de las líneas de la imagen al dibujarlas en la pantalla, según la curvatura de la ruta y la posición relativa de la moto sobre la misma. Este componente es nuevo en este trabajo.

Figuras:

Son las figuras que se dibujan sobre la pantalla que corresponden a los objetos en movimiento como árboles, carteles, la moto, etc. y son las que dan la sensación de profundidad. Estas imágenes se generaban con el chip de Super Scaler, que podía posicionar una figura con cualquier tamaño en cualquier posición de la pantalla. Las herramientas para escalar y posicionar ya fueron desarrolladas en los ejercicios previos, la lectura de las figuras desde los archivos de ROMs son parte de este trabajo.

Textos:

Finalmente los textos se sobreimprimen en la pantalla para dar información contextual sobre el juego. Se generaban con los chips de tiles con los que se dibujaban los fondos y esta funcionalidad ya fue presentada en el EJ4 como parte del main() provisto por la cátedra.

La ilusión de movimiento de un juego se consigue regenerando la composición de esta imagen varias veces por segundo (específicamente 30 en el juego original) y presentándola al jugador, posicionando los elementos de la escena según la interacción del jugador.

El juego

Como ya se dijo el juego Hang-On es un juego de carreras de motos. El objetivo del juego es llegar desde la largada a la llegada conduciendo la moto sobre una ruta con una serie de curvas y obstáculos a los márgenes. La moto tiene controles muy sencillos: Giro hacia la derecha y la izquierda, aceleración y frenado.

Cabe señalar que en el juego original la lógica y la potencia de cómputo para esta lógica era tremendamente acotada y la misma es muy sencilla. El fuerte del juego era la parte gráfica que vendía la ilusión de la simulación y es lo que garantizó el éxito del arcade y de la arquitectura.

Resumiendo, la moto se encuentra sobre una ruta. El acelerador acelera la velocidad, el freno la reduce, mientras la moto se mueve avanza una determinada distancia en cada instante de tiempo, y al avanzar los elementos del entorno se mueven de forma relativa con respecto a la posición de la moto.

Desde el punto de vista de la representación del juego en realidad la moto está siempre fija en el mismo lugar y lo que se mueve es el entorno. Es decir, vamos a representar la moto según su distancia desde la largada y su posición con respecto al centro de la ruta. Si la ruta dobla hacia la derecha impulsará a la moto hacia la izquierda y viceversa. Consistentemente con esto, la moto siempre se dibuja en el centro de la pantalla y es la perspectiva de los demás objetos lo que se modifica para reflejar la posición relativa.

El objetivo del juego es llegar a la meta antes de que se termine el tiempo.

Nuevas ROMs y formatos

Rutas

La ruta está contenida en la ROM 6840.rom y en sus 32KB codifica 4 imágenes de 512x128 pixeles, las cuales cada una es un bit de color de la ruta.

¡Momento!, ¿dijimos 4 bits de color?, sí, pero la realidad es que si bien el hardware contempla 4 bits en realidad se utilizan sólo dos, es indistinto levantar los 4 bits o levantar los 2 que efectivamente se emplean.

El formato es un volcado de los bits de las imágenes de izquierda a derecha y de arriba a abajo. Cada imagen será una sucesión de 65536 bits, o sea, 8K bytes.

Para referencia, la ROM completa tiene este aspecto:

Mientras que los 4 bits compuestos como valores de gris (sin ningún orden particular) tiene este aspecto:

Notar que las rayas del centro y los márgenes de la ruta se generan después mediante la elección de una paleta adecuada de acuerdo a la profundidad. Notar, además, que sólo se define la mitad de la ruta, para dibujarla completa la misma se espeja horizontalmente y se dibuja superponiendo los 8 pixeles centrales.

Si bien la ROM completa define una ruta de 512x128, parte de esta ruta no se utiliza en el juego. La ruta real tendrá una altura de 96 pixeles, descartando las primeras y últimas 16 filas.

Hay una particularidad y es que la ruta define para el "fondo" el mismo color que para la raya central. Dado que queremos que el fondo sea transparente pero no el centro, hay que reemplazar a izquierda todos los valores con todos los bits en 1 por 0 hasta que se encuentre el primer valor de diferente color, que es el borde de la ruta.

Figuras

Las figuras se encuentran contenidas en las ROMs que van del 6819 al 6830 y luego del 6845 al 6846.

Estas ROMs representan un bloque contínuo de memoria de tipo uint16_t donde como cada ROM tiene 32KB y hay 7 pares de ROMs serán entonces 229376 valores de 16 bits.

Las ROMs están interlineadas, esto quiere decir, que el primer byte de la ROM 6819.rom se corresponde al byte bajo del primer valor, mientras que el primer byte de la ROM 6820.rom se corresponde al byte alto. La ROM 6819 aporta todos los bytes bajos de los primeros 32768 valores mientras que la ROM 6820 aporta todos los bits altos de estos mismos valores. Así para cada ROM, por ejemplo, el primer byte de la ROM 6821.rom aporta el byte bajo del valor 32769.

Estas ROMs deben ser cargadas en memoria en un único vector uint16_t rom[229376] para poder ser accedidas para extraer las respectivas figuras allí contenidas.

Formato de las figuras

Cada una de las figuras están representadas en la memoria de las rom con paletas de 4 bits. Cada uint16_t de la ROM representa 4 pixeles abcd según el siguiente esquema:

15                                        7                                     0
+----+----+----+----+----+----+----+----++----+----+----+----+----+----+----+----+
| a3 | a2 | a1 | a0 | b3 | b2 | b1 | b0 || c3 | c2 | c1 | c0 | d3 | d2 | d1 | d0 |
+----+----+----+----+----+----+----+----++----+----+----+----+----+----+----+----+

El archivo no define ni la ubicación ni la altura de las diferentes figuras, si no que el programa debe saber en qué posición de la rom encontrarlas.

Cada figura es una sucesión de líneas, las cuales tienen longitud variable; por ejemplo, la secuencia:

{0xf0fe, 0x0f0f, 0xf0ee, 0xef0f, 0xf07e, 0x170f, 0xf422, 0x440f, 0xfabb, 0xae0f, 0xf05b, 0x240f, 0xf04c, 0x7b0f, 0xf0b9, 0xba0f, 0xf0ab, 0xaf0f}

define una imagen de (y esto no está contenido en la rom) 9 líneas de alto.

Cada línea es una sucesión de números de 16 bits que representan 4 pixeles abcd hasta que se encuentra un valor de d igual a 0xf. Este valor es el disparador de que comienza una nueva línea. Repitiendo la secuencia separando por líneas tenemos entonces:

{0xf0fe, 0x0f0f,
0xf0ee, 0xef0f,
0xf07e, 0x170f,
0xf422, 0x440f,
0xfabb, 0xae0f,
0xf05b, 0x240f,
0xf04c, 0x7b0f,
0xf0b9, 0xba0f,
0xf0ab, 0xaf0f}

(En este ejemplo todas las líneas tienen exactamente 2 palabras de 16 bits de ancho, pero esto no tiene por qué ser así.)

Nota

En muchos lugares de la ROM después de una nueva línea vienen secuencias 0x0f0f las cuales "crearían" otra nueva línea. Si empezando una nueva línea viniera un valor (o varios) que disparan nueva línea deben dejarse pasar.

Tanto los valores de los pixeles en 0x0 como en 0xf se consideran transparentes, es decir, como si valieran 0. Entonces, sabiendo que cada fila tiene 7 pixeles de ancho (sin hilar muy fino, pero son 2 números que representan 4 pixeles cada uno y el último pixel sólo indica nueva línea; si miramos más en detalle vamos a ver que en realidad la imagen tiene 6 pixeles de ancho, pero no nos importa, la última columna podemos considerarla transparente y simplificar), podemos extraer la imagen como:

{{0, 0,  0, 14,  0,  0,  0},
{0,  0, 14, 14, 14,  0,  0},
{0,  0,  7, 14,  1,  7,  0},
{0,  4,  2,  2,  4,  4,  0},
{0, 10, 11, 11, 10, 14,  0},
{0,  0,  5, 11,  2,  4,  0},
{0,  0,  4, 12,  7, 11,  0},
{0,  0, 11,  9, 11, 10,  0},
{0,  0, 10, 11, 10,  0,  0}};

En la siguiente imagen podemos verla representada a la izquierda en escala de grises con sus 4 bits y a la derecha aplicando una paleta de 12 bits:

Este es el formato para todas las figuras. Como ya se dijo, es dato la posición de inicio y la cantidad de filas que abarca (y, por simplificar, la cantidad de columnas también es conocida, pese a que puede obtenerse de la memoria).

Especificación

Tamaños, posiciones, cifras, etc.

Intentaremos centralizar todos los números de interés en esta sección:

Tamaño de la pantalla:

320x224

Centro vertical de la pantalla:

x=162 (sí, totalmente deducible de que la pantalla tiene 320px de ancho...)

Tamaño del área del cielo:

320x128, superior

Tamaño área del terreno:

320x96, inferior

Fondo2:

1216x64, se apoya en el terreno así que la fila superior está en y=64

Fondo1:

1728x16, se apoya en el terreno así que la fila superior está en y=112

Relación entre los dos fondos:

\(\frac{1728 + 320}{1216 + 320} = 0.75\). Esta es la relación entre los desplazamientos de ambos al moverse. La idea es que ambos fondos entren juntos por la derecha y salgan juntos por la izquierda.

Ruta:

La ruta tiene 96 pixeles útiles de alto. Como ya se dijo, de la ROM se descartan 16 pixeles de arriba y 16 de abajo de los 128 que la definen. La ROM sólo representa una mitad de la ruta, por lo que hay que reflejarla, teniendo una superposición de 8 pixeles en el medio. Es decir, el borde de la derecha de la mitad izquierda termina en la posición 162 + 4 y recíprocamente el borde de la izquierda de la mitad derecha está en 162 - 4, garantizando con eso 8 pixeles de superposición. Siendo que la imagen tiene 512 de ancho, entonces la mitad izquierda se dibuja en \(x = 162 + 4 - 512 = -346\) y la mitad derecha en \(x = 162 - 4 = 158\).

Todas estas posiciones están dadas para la ruta sin transformar, es decir, con un tramo en línea recta y la moto ubicada en el centro.

Textos:

Se deja libertad para ubicar los textos de forma aproximada a cómo están en el juego original. Cabe destacar que en el juego original están ubicados en posiciones redondas del tamaño de la tesela, o sea múltiplos de 8.

Las letras, números y el espacio están en las posiciones dadas por la tabla ASCII.

Los números de los segundos restantes del tiempo empiezan en la tesela 0x80, estando la mitad superior del 0 en 0x80 y la inferior en 0x81 y a continuación el resto de los números.

El texto de "TOP" va de la tesela 0x97 a la 0x9b el borde superior izquierdo en 0x94, superior medio 0x95, superior derecho 0x96 (es decir, para generar el borde superior completo hay que escribir "x94x95x95x95x96"), análogamente el inferior va del 0x9c al 0x9e con el mismo criterio.

"SCORE" borde superior entre 0xb0 y 0xb2, texto entre 0xb3 y 0xb9, y borde inferior entre 0xba y x0bc.

"TIME": superior: 0xa0-0xa2, texto: 0xa3-0xa8, inferior: 0xa9-0xab.

"GAME OVER": son dos filas, la primera va de 0x60 a 0x6f y la segunda de 0x70 a 0x7f.

"GOAL": son dos filas, la primera de 0xe0 a 0xe7 y la segunda de 0xe8 a 0xef. (Además del texto GOAL en las teselas hay una figura que también puede usarse para el mismo fin.)

Todos los textos usan las paletas 5, 6 y 7 del EJ4.

Perspectiva

La perspectiva cubre cómo mapear las posiciones y escalas de los diversos objetos en la pantalla para dar la impresión de tridimensionalidad.

Todos los objetos están representados por coordenadas de distancia al centro de la ruta y distancia a la moto y tienen un tamaño propio. Como la moto está siempre en el centro de la pantalla y avanzando entonces todos los objetos se ubicarán en la pantalla con respecto a esta referencia.

Entonces, todo va a ser relativo al centro de la ruta... ¿cómo se ubica pues el centro de la ruta?

En la esquina superior izquierda de la siguiente imagen se ve la ruta como está en la ROM, dibujada reflejada y superpuesta:

La ubicación del centro de la ruta va a dar completo el efecto de la perspectiva y van a utilizarse dos modificaciones para generar este efecto:

Desplazamiento lateral:

En el desplazamiento lateral el punto de fuga seguirá en el medio pero todo se desplazará linealmente según la posición de la moto en la posición contraria. Es el efecto que se ve en la esquina superior derecha de la imagen anterior.

Desplazamiento por curva:

En el desplazamiento por curva la imagen va a apartarse del centro conforme se aleje de la pantalla. Es el efecto que se ve en la esquina inferior izquierda.

Ambos efectos:

La adición de ambos efectos es lo que se ve en la esquina inferior derecha.

Es decir, la ruta no se pegará en la pantalla como es, si no que cada una de sus filas se pegará en una posición particular.

Variables

Para no confundirnos con la nomenclatura vamos a ponerle nombre a las variables y a los ejes.

Sobre la pantalla vamos a referir todo con respecto a la posición de la moto en la pantalla. La moto está abajo en el medio y ahí vamos a fijar nuestro origen de coordenadas para las variables \(u\) y \(v\), siendo \(u\) la variable que crece hacia la derecha y \(v\) hacia arriba. Como es de esperar, la \(v\) va a estar acotada entre 0 y 95, porque es el espacio que ocupa la ruta. La \(u\) puede moverse entre valores positivos y negativos, y las cuentas pueden hacer que caigan fuera de la pantalla.

Sobre la ruta vamos a referir todo con respecto a la distancia \(x\) desde la largada y la distancia \(y\) con respecto al centro de la ruta. Todos los objetos estarán definidos en función de sus coordenadas \(x\) e \(y\), siendo la moto la única que va a modificar esas coordenadas durante el juego, avanzando sobre el eje \(x\) y girando sobre el \(y\).

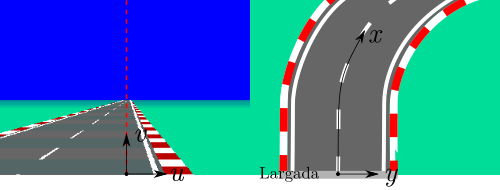
Notar que el 0 de \(v\) se corresponde con la posición \(x_m\) de la moto en ese instante. Para el resto de los objetos al dibujarlos nos interesará saber a qué distancia de la moto se encuentran, porque esa distancia es la que mapearemos en el eje \(v\).

Ecuaciones

Si definimos \(d\) como la distancia hacia adelante de la moto de cualquier cosa, es decir \(d = x_x - x_m\), nos interesa saber dónde se ubicará ese objeto en la pantalla. Se propone la siguiente fórmula:

\[v(d) = \left\lfloor 96 - 96 e^{-0.11 d} \right\rfloor.\]

Notar que objetos con \(d < 0\) están detrás de la visión y no dan valores válidos de \(v\) mientras que lo demás está entre 0 y 95.

Restringiremos el campo de visión a 60 metros, por lo que todo lo que tenga \(d > 60\) no se dibujará.

Análogamente nos interesará tener la inversa de esta función, para saber a qué distancia se encuentra algo que está en determinada posición. Invirtiendo la ecuación anterior obtenemos:

\[d(v) = -\frac1{0.11}\ln\left(\frac{96-v}{96}\right).\]

Ahora bien, los objetos tienen una determinada altura \(h_0\) que está referida a lo que ocupan cuando \(v = 0\). Cabe preguntarse cómo se escalan cuando están a una determinada distancia. Dado que esta proporción tiene que ver con la perspectiva y que ya metimos nuestra perspectiva en el cálculo de la posición en \(v\) referiremos esta relación con respecto a esta última variable:

\[h(v) = h_0 \frac{96 - v}{96} + \frac{5v}{96}.\]

El ancho debe escalarse proporcionalmente al escalamiento en la altura. Si con esta cuenta el ancho diera menor a 3 pixeles se debe forzar en 3.

Volviendo a los desplazamientos, con estas coordenadas, los desplazamientos (en verde en el dibujo) pueden esquematizarse de esta forma:

donde los desplazamientos van a afectar la posición de la coordenada \(u\). Como ya se dijo, la transformación de la ruta será la suma de ambos desplazamientos.

Teniendo la moto una posición con respecto al centro de la ruta \(y_m\), el desplazamiento lateral de la ruta se puede calcular como:

\[u_l(v) = -y_m \frac{96 - v}{96}.\]

Cuando \(v = 0\) se tiene un desplazamiento igual a la posición de la moto, y este desplazamiento se achica hasta desaparecer en el horizonte.

Para hablar del desplazamiento de curva hace falta mencionar un poco de cómo se define la ruta. La ruta se definirá de a tramos de 1 metro, especificando en cada tramo su radio de curvatura en una unidad adimensionalidad (como referencia, una curva suave tendrá radio 1). Un radio de 0 indica una ruta recta, radios positivos giro a la derecha y radios negativos giro a la izquierda. Como es esperable, el desplazamiento de curva estará relacionado con el radio de los tramos de ruta venideros.

Como la ruta tiene transiciones, el cómputo del desplazamiento de curva tiene que hacerse acumulativo con los radios de los diferentes tramos que se observan. Para cada valor de \(v\) puede saberse a qué tramo representa dado que se conoce la posición \(x_m\) de la moto y puede obtenerse la posición de ese tramo como \(x_m + d(v)\).

El desplazamiento lateral se curva como:

\[u_c(0) = 0,\]

\[u_c(v) = u_c(v - 1) + r(v) e^{0.105 v - 8.6}\]

siendo \(r(v)\) el radio de curva de la ruta en el punto que se corresponde a esa \(v\).

El desplazamiento del centro de la ruta va a ser la suma \(u_r(v) = u_l(v) + u_c(v)\), la idea es computar este vector de 96 posiciones una vez por cada instante dado que el mismo no sólo sirve para dibujar la ruta sino, como ahora veremos, también sirve para posicionar el resto de los objetos en la pantalla.

Volviendo a los objetos, para posicionar una figura en la pantalla tenemos su posición en \(v\), su altura \(h\) y nos falta conocer su posición \(u\). Esta posición será computada como:

\[u = y_x \frac{96 - v}{96} + y_x \frac{v}{5000} + u_r(v),\]

donde \(y_x\) es su distancia al centro de la ruta y \(u_r\) y el desplazamiento total del centro de la ruta.

Figuras

Se provee el siguiente listado de figuras que se pueden obtener de la rom:

Moto 1:

Inicio: 532, ancho: 36, alto: 73

Moto 2:

5670, 36, 70

Moto 3:

11284, 46, 63

Moto 4:

17215, 60, 54

Árbol:

50116, 46, 188

Cartel:

37390, 96, 112

Roca:

69464, 136, 76

Cartel Bell:

82922, 63, 146

Cartel Forum:

89102, 118, 114

Cartel Delfín:

119280, 144, 110

Semáforo:

108724, 66, 201

Banner largada:

114518, 244, 48

Viga banner:

127098, 198, 48

Texto GOAL:

Si no se usa el texto de las teselas, puede usarse la figura que está en 194556, 140, 47. El juego original utiliza la paleta_4[28] pero hay otras que le quedan igualmente bien (o, mejor dicho: le quedan mejor).

Las cuatro figuras de la moto son la moto vertical y las distintas posiciones intermedias de doblado.

Paleta

Se provee una nueva versión de paleta.c la cual incorpora la tabla paleta_4 que contiene las paletas de 4 bits para ser usada con las figuras.

Además se proveen los siguientes colores que son los que se utilizan para pintar la ruta. No se dan como una paleta ya armada porque se dejó libertad a la hora de levantar la ROM de la ruta, por lo que las posiciones de las columnas pueden variar, reordenarlas según corresponda:

const pixel_t colores_ruta[4][4] = {
    // columnas: Asfalto, líneas laterales, color lateral, franja del medio
    {0x666, 0xfff, 0xb00, 0xfff},
    {0x666, 0xfff, 0xfff, 0xfff},
    {0x566, 0xfff, 0xb00, 0x566},
    {0x566, 0xfff, 0xfff, 0x566}
}

Ruta

La ruta se va a definir según un vector con los tramos de la misma, un tramo por cada metro. En total la ruta tiene 4200 metros, por lo que esa será la longitud.

Cada tramo de ruta se representará según esta estructura:

struct ruta {
    float radio_curva;
    size_t indice_figura;
};

donde el indice_figura valdrá 9999 de no haber una figura asociada a ese tramo.

Entonces la ruta estará definida como struct ruta ruta[4200];. (En realidad se agregaron 70 tramos más de ruta recta al final para no tener que complejizar la lógica de dibujado al llegar al final, como el horizonte es de 60 metros hay todavía un margen de 10 antes de acceder a posiciones por fuera del vector.)

Cada figura de la ruta será una estructura del siguiente tipo:

struct figura_en_ruta {
    enum figura figura;
    size_t paleta;
    int y;
    bool reflejar;
};

El enumerativo tendrá al menos las siguientes claves:

{ARBOL, CARTEL, ROCA, BELL, FORUM, DELFIN}

pudiendo el alumno agregar las que le sean convenientes.

La paleta indicará con qué paleta se dibuja esa figura, y será la distancia al centro de la ruta, y reflejar indicará si la figura tiene que ser reflejada horizontalmente. Notar que no se provee la x la cual se obtiene de la ubicación en la ruta ni la h0 la cual es la altura de la figura en cuestión y ya es conocida.

Se provee un struct figura_en_ruta figuras_en_ruta[]; que referencia las figuras de la ruta.

Notar que el semáforo, que tiene que mostrarse tanto en la partida como en la llegada no se va a asociar a la ruta. Esto es porque el mismo se dibuja con 5 figuras en el mismo tramo y además porque la animación se hace cambiando la paleta. Eso deberá ser manejado por fuera.

Nota

No se hizo esta aclaración hasta el momento así que este es tan adecuado como cualquier otro pero: Las figuras se referencian todas con respecto a su coordenada de abajo en el medio, o sea, centrada en las equis y con respecto a su base.

Tomar en cuenta que las primitivas de imagen_t usan posiciones con respecto a la esquina superior izquierda. Por lo que al pegar figuras habrá que restarle a las yes el alto de la figura y a las equis la mitad del ancho.

Física del juego

Como ya se dijo lo sólido de la arquitectura System 16 eran los gráficos, por lo que la simulación física real es bastante sencilla y apenas son un par de reglas simples.

La física del juego se evalúa en cada instante de tiempo, a una tasa de FPS cuadros por segundo. Por lo tanto entre cada instante transcurren \(\Delta t = \frac1{\mathrm{FPS}}\).

La moto tiene 4 controles: Acelerar, frenar, derecha, izquierda. Estos controles son de caracter permanente, por ejemplo, si el jugador aprieta el acelerador la moto tiene que pasar a un estado de acelerada y seguirá acelerando hasta que el usuario suelte el acelerador. Es decir, no es que se censa cada vez que se aprieta el acelerador sino cuando se aprieta y cuando se suelta.

Estas son las reglas, ordenadas de forma arbitraria:

Posición \(m_x\):

La posición se actualizará en cada instante según la velocidad y el paso temporal. Tomar en cuenta que la velocidad se mide en km/h mientras que al posición se mide en metros, por lo que hay que convertir las unidades.

Aceleración:

Si está presionado el acelerador o si la moto está a menos de 80 km/h entonces se acelera según:

\(v_{i+1} = 279 - (279 - v_i) e^{-0.224358 \Delta t}\)

Frenado:

Por cada segundo que el freno esté presionado se le restan 300 km/h a la velocidad.

(Podemos asumir que no se presionan acelerador y freno a la vez, en el juego original el freno le gana al acelerador.)

Desaceleración:

Si no se está presionando ni el acelerador ni el freno por cada segundo transcurrido se le restan 90 km/h a la velocidad.

Morder la banquina:

Si la posición \(m_y\) es superior a 215 metros (en módulo) y además la velocidad es superior a 92 km/h entonces en ese instante se le restan 3 km/h a la velocidad.

Giro:

Hay tres intensidades de giro para cada lado y una posición neutral.

Giro a la derecha:

Si está presionado el giro a la derecha y todavía no se alcanzó la tercera intensidad de giro a la derecha, se incrementa el giro en esa dirección.

Giro a la izquierda:

Análogo al giro a la derecha.

Reposo:

Si no está presionado ningún giro pero todavía hay intensidad de giro en alguna dirección entonces se bajará la intensidad una unidad.

Posición \(m_y\):

La posición se incrementa en 3, 9 o 15 metros según la intensidad del giro, en la dirección que corresponda.

Irse al pasto:

Si \(m_y\) es mayor a 435 en módulo, entonces se fuerza en 435 con el signo que corresponda.

Giro de la ruta:

Siendo \(\Delta x = x_{i+1} - x_i\) la distancia avanzada en el paso de tiempo actual, la posición sobre la ruta se actualizará según la cantidad:

\(2.5 \Delta x \, r(m_x)\)

Siendo \(r\) el radio de la curva en esa posición.

Puntaje:

El puntaje se computa como \(125 \Delta x\) si la moto circula a menos de 117 km/h y como \(\Delta x (3.13 v - 240)\) si la velocidad \(v\) es superior.

En caso de estar mordiendo la banquina no se suma ningún punto.

Ganar:

Se gana si se llega al final de la ruta en 4200 metros.

Perder:

Se pierde si se acaban los 75 segundos y no se llegó a la llegada.

Choques:

Si la posición de la moto está entre el lado izquierdo y el derecho de una figura (no nos olvidemos de que la y de las figuras está en el centro) y la figura está a menos de \(\lfloor 77.5 \Delta t + 1 \rfloor\) metros de distancia de la moto se produce un choque. Cuando se choca la moto vuelve a \(y_m = 0\) con velocidad 0 y el juego se queda detenido durante 5 segundos.

(Esta distancia en metros se toma siendo la velocidad máxima de 279 km/h, por ejemplo a una tasa de 30 cuadros por segundo esta cuenta da 3 metros siendo que la moto recorre como máximo 2,58 metros por cuadro.)

Notar que a menos que se indique lo contrario estas reglas no son excluyentes, por ejemplo, que la ruta gire no anula que el usuario además esté haciendo girar la moto para compensar, precísamente, ese giro de la ruta. Se aplican ambos efectos en simultaneo.

Tres observaciones sobre imagen_t

1. En la lógica del juego actual se hace un uso muy intensivo de la primitiva de pegar y pegar con paleta y hay que optimizar para no iterar de más. Por eso no puede usarse iterar el tamaño completo del origen y verificar límites dentro de la iteración si no que se deben ajustar los límites de iteración para iterar sólo lo necesario.

   El ciclo de iteración corregido debería tener un aspecto así:

   for(int f = y >= 0 ? 0 : -y; f < origen->alto && f + y < destino->alto; f++)
       for(int c = x >= 0 ? 0 : -x; c < origen->ancho && c + x < destino->ancho; c++)
           ...
   

   debíendose todavía chequear la transparencia para cada pixel.

2. Hay varias partes de la aplicación que necesitan reflejar horizontalmente una imagen. El reflejo se puede hacer como una primitiva que refleje una imagen y ya, pero también se puede integrar a la primitiva de pegado con paleta. En el caso de hacerlo en la primitiva de pegado con paleta se ahorra crear imágenes adicionales que después hay que destruir.

3. La biblioteca gráfica SDL2 representa una textura de MxN como un vector uint16_t v[M*N]; donde cada posición es un pixel de izquierda a derecha y de arriba a abajo en formato RGB444. Por lo tanto hace falta agregar una primitiva muy sencilla que sea:

   void imagen_a_textura(const imagen_t *im, uint16_t *v);
   

   que vuelque cada pixel de im en el vector v.

Coloreado de la ruta

Cada metro de la ruta se colorea con cada una de las cuatro paletas dadas, repitiendo los colores cada cuatro metros.

Al dibujar la ruta se sabe la posición que corresponde al \(x_m\) en ese instante, y para cada franja de la ruta se puede computar \(x_m + d(v)\) con lo cual se obtiene la posición exacta que se corresponde con esa franja.

La paleta se debe aplicar cíclicamente cada 4 metros de esa posición.

Dibujado del fondo

Como se mencionó antes, al inicio ambos fondos están exactamente a la derecha del borde de la pantalla. Al girar la ruta el fondo1 tiene que moverse exactamente la cantidad de radio de curva acumulado hasta el momento, mientras que el fondo2 las tres cuartas partes de esta cantidad.

Siendo que el radio de curvatura es positivo a la derecha y se espera que el fondo se desplace hacia la izquierda, la acumulación se tiene que hacer con signo negativo.

Cuando se haya girado tanto a la izquierda que la ubicación del fondo supera los 320 pixeles debe ubicarse de vuelta a la izquierda. Es decir, los fondos tienen que dar el efecto de abarcar 360º con un bache de 320 pixeles entre inicio y fin.

Cabe destacar que la suma de todos los radios de giro es 2048, por lo que al terminar el nivel el fondo tiene que estar exactamente en 320 pixeles de posición como al inicio.

Semáforo

Como se dijo el semáforo es la combinación de cinco figuras:

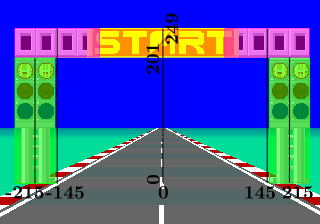
Hay un detalle y es que las figuras del banner y la viga tienen 48 px de alto pero deben dibujarse en la altura. Se recomienda hacer algo tipo:

viga = imagen_generar(198, 249, 0);
imagen_pegar(viga, viga_como_esta_en_la_rom, 0, 0);
imagen_destruir(viga_como_esta_en_la_rom);

es decir, pegarlo en una imagen más grande de tal manera que tenga 201 pixeles transparentes debajo. Haciendo esto puede pegarse perfectamente en la largada y la llegada con las mismas rutinas que se usan para pegar todas las demás figuras.

La paleta para la viga es la número 45. Para el banner la paleta 45 muestra el cartel de "START" y la paleta 47 el de "GOAL". El semáforo tiene 4 paletas: 41, 42, 43, 44 que son: apagado, rojo, amarillo y verde respectivamente.

Dibujo de la moto

La moto usa las paletas 0, 1, 2 y 3. A medida que la moto se mueve se alternan las paletas 0 y 1 en función de la velocidad para simular el movimiento de la rueda. Las paletas 2 y 3 tienen la luz de freno prendida y se alternan del mismo modo. Si por cada metro recorrido se alternan dos veces la paleta el efecto se parece al del juego original.

Cuando la moto gira hay que hacer una transición desde la figura Moto 1 a Moto 4 pasando por las intermedias. Notar que Moto 1 y Moto 2 tienen 36 pixeles de ancho, por lo que para dibujarlas centradas hay que hacerlo con un margen de 18 pixeles. Bueno, el mismo margen se usa para Moto 3 y Moto 4, quedando la imagen descentrada. (Es decir, si la moto girara a la derecha se grafican todas en x = 162 - 18 --y si girara a la izquierda rehacer la cuenta para que quede simétrica--.)

Trabajo

Ya se dijo todo lo que había por decir. Tenemos implementado el TDA imagen_t y ya estamos familiarizados con las paletas, teselas y mosaicos. En el TP se busca incorporar las figuras y la ruta y hacer uso intensivo de las primitivas de imágenes para componer la escena.

El problema que se plantea en este trabajo deberá ser resuelto con las herrramientas ya adquiridas, extendiendo de forma consistente los TDAs ya planteados de ser necesario y diseñando los TDAs nuevos que hagan falta. Se evaluará además el correcto uso de los TDAs respetando la abstracción y el "modelo" de Alan-Bárbara, así como la separación de los cómputos físicos con respecto a la lógica de representación gráfica.

Se pide diseñar una aplicación que pueda ser ejecutada como:

$ ./hangon

que permita jugar al juego Hang-On, con toda la lógica del problema y que sea capaz de informar al usuario del tiempo, su puntaje, velocidad, etc.

Se deben implementar TDAs donde se considere que es necesario.

Al menos la Moto tiene que ser implementada como un TDA con sus características como la posición, velocidad, y los detalles que necesiten tener memoria.

La lógica del juego es totalmente independiente de la representación gráfica de los objetos, el cómputo de ambos mundos debe ser independiente entre sí.

El alcance inicial del juego es el especificado y una buena implementación del mismo es suficiente para alcanzar la máxima nota. La prioridad es resolver completa esta funcionalidad descrita para terminar con eso la materia.

Ahora bien, por simplificar el enunciado se dejaron afuera de la especificación muchos detalles del juego original que pueden ser implementados como puntos adicionales.

Material

Fuentes varios

Se proveen los archivos de paletas, fondos, ruta, las ROMs y un ejemplo de SDL2 en: archivos_20222_tp1.tar.gz

Valgrind

En el caso de una aplicación construída con SDL2 se hace complejo el uso de Valgrind porque esta biblioteca tiene desprolijidades en su implementación que hacen que Valgrind tire múltiples errores y estos errores a la tasa que marquen los FPS del juego. Por eso para poder testear con Valgrind sobre el código desarrollado tenemos que suprimir los errores que son relativos a SDL2.

Se provee el siguiente archivo de supresiones para Valgrind: suppressions_20222_tp1.supp

Con este archivo descargado Valgrind puede ser invocado como:

$ valgrind --suppressions=suppressions_20222_tp1.supp --leak-check=full ./hangon

con lo que el programa se ejecutará suprimiendo los millones de errores de SDL2.

Al haber errores y haberlos suprimido el reporte no será del todo satisfactorio, y va a haber memoria en el heap y elementos marcados como "still reachable". El siguiente es un reporte de ejemplo:

==27213== Memcheck, a memory error detector
==27213== Copyright (C) 2002-2017, and GNU GPL'd, by Julian Seward et al.
==27213== Using Valgrind-3.13.0 and LibVEX; rerun with -h for copyright info
==27213== Command: ./hangon
==27213==
==27213==
==27213== HEAP SUMMARY:
==27213==     in use at exit: 196,326 bytes in 1,058 blocks
==27213==   total heap usage: 32,817 allocs, 31,759 frees, 118,233,488 bytes allocated
==27213==
==27213== LEAK SUMMARY:
==27213==    definitely lost: 0 bytes in 0 blocks
==27213==    indirectly lost: 0 bytes in 0 blocks
==27213==      possibly lost: 0 bytes in 0 blocks
==27213==    still reachable: 2,037 bytes in 10 blocks
==27213==         suppressed: 194,289 bytes in 1,048 blocks
==27213== Reachable blocks (those to which a pointer was found) are not shown.
==27213== To see them, rerun with: --leak-check=full --show-leak-kinds=all
==27213==
==27213== For counts of detected and suppressed errors, rerun with: -v
==27213== ERROR SUMMARY: 0 errors from 0 contexts (suppressed: 1018824 from 25)

Notar que pese a que se señala más de un millón de errores, el reporte de pérdidas dice que no hay bloques ni definitiva, ni indirecta ni posiblemente perdidos. Además el reporte, pese a haber sido corrido con --leak-check=full no muestra ningún error en nuestro propio código.

Se busca que el reporte tenga estas características.

Ahora bien, prestar atención porque ignorar los errores de still reachable puede enmascarar errores como por ejemplo no haber llamado a fclose() entre otros.

Nota

Ejecutar con Valgrind implica a poner a un programa a analizar cada cosa que hace nuestro programa. Con un programa pesado en cantidad de operaciones como el nuestro, el programa va a andar muy lento.

La idea es correr con Valgrind como un chequeo a realizar, pero no todo el tiempo durante del desarrollo.

Para liberar la carga, sólo durante las corridas de Valgrind, se puede reducir el valor de JUEGO_FPS a un valor que lo haga más manejable. Esto va a alterar un poco la física del juego (pese a que todas las cuentas son proporcionales a \(\Delta t\)), pero al menos va a permitir testear más intensivamente la memoria.

Funcionamiento

Las ecuaciones y formuleos presentados son casi fieles a los del original, por lo que la recomendación es que juegues el juego original para entender la mecánica del mismo.

Dado que se hicieron múltiples simplificaciones en lo visual se grabó este video con los parámetros implementados por la cátedra:

(Es claramente visible un bug llegando al final del juego en la primera vuelta, a ver quién se da cuenta.)

Entrega

Requisitos

Los únicos requisitos son que el programa resuelva correctamente la funcionalidad pedida y que lo haga utilizando TDAs con un diseño planificado a conciencia. Si hacés eso nada puede salir mal.

Entregables

Deberá entregarse:

1. El código fuente del trabajo debidamente documentado.

2. El archivo Makefile para compilar el proyecto.

Nota

El programa debe:

• estar programado en C,

• estar completo,

• compilar...

• sin errores...

• sin warnings,

• correr...

• sin romperse...

• sin fugar memoria...

• resolviendo el problema pedido...

Trabajos que no cumplan con lo anterior no serán corregidos.

La entrega se realiza a través del sistema de entregas.

El ejercicio es grupal permitiéndose grupos de hasta 2 integrantes.

Si elegís hacer el trabajo en grupo te pedimos que nos avises o por mail o por Discord quién es tu compañero de grupo así lo cargamos en el sistema de entregas. (Si el grupo sufriera alteraciones avisanos también.)