Ejercicio obligatorio 1
Fecha de entrega: Lunes 3 de abril
Nota
Nunca es buena idea empezar por un ejercicio integrador antes de tener practicados los temas que el trabajo integra.
Se sugiere antes de desarrollar este trabajo resolver, al menos, los siguientes ejercicios de la guía de Introducción al lenguaje C:
Ejercicio 1 (interés compuesto).
Ejercicio 4 (cantidad de segundos).
Ejercicio 13 (tabla del 7).
Ejercicio 18.c (exponencial).
Introducción
Para un sistema físico sabemos de la primera ley de Newton que \(\sum \vec F = 0\). En un sistema masa-resorte podemos plantear que las fuerzas presentes son la fuerza del resorte y la fuerza que ejerce la masa. Para la primera de ellas, podemos utilizar la ley de Hooke, que dice que la fuerza será proporcional al estiramiento por la constante de elasticidad del resorte, mientras que para la segunda de ellas podemos aplicar la segunda ley de Newton que nos dice que la fuerza será igual a su masa por su aceleración.
Si tuviéramos un sistema como este, con este sistema de referencia:
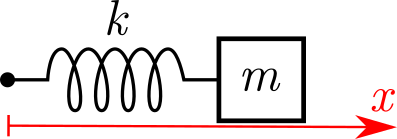
entonces podemos plantear el sistema como:
donde indicamos como \(\ddot{x}\) a la derivada segunda de \(x\) con respecto al tiempo, o sea, la aceleración.
Si quisiéramos resolver este sistema de forma analítica deberíamos resolver esta ecuación diferencial de segundo grado, pero no lo haremos porque en cambio nos interesa resolver la evolución del sistema de forma numérica.
En una resolución numérica generalmente discretizamos el tiempo en intervalos de \(\Delta t\) y resolvemos desde un instante \(t_0\) para cada uno de los \(t_i\) subsiguientes. Es decir, vamos a resolver para una serie de tiempos donde \(t_{i + 1} = t_i + \Delta t\).
Entonces lo que vamos a obtener es para cada tiempo \(t_i\) la posición \(x_i\) de la masa.
¿Para qué nos sirve discretizar el tiempo?, nos sirve como una manera de resolver de forma algebraica las derivadas, si tenemos una función \(x(t)\) sabemos del CBC que su derivada se calcula como
Ahora bien, si omitimos el límite y le damos a \(h\) algún valor particular podemos obtener una aproximación que mejorará a medida que reduzcamos más y más ese valor. Convenientemente podemos tomar \(h = \Delta t\) y nos quedará:
y discretizando e introduciendo la notación que usamos antes podemos reescribir como:
Esta es la idea del método. Si este término estuviera en el contexto de una ecuación podríamos obtener el valor subsiguiente de \(x\) en función de sus valores anteriores. No vamos a seguir este razonamiento, pero es importante entender la idea general para entender lo que viene.
Este método puede extenderse a derivadas segundas y puede escribirse de esta forma:
Volviendo a nuestro problema inicial, podemos aplicar esta expansión de la derivada segunda en nuestra ecuación de la masa-resorte, discretizarla en tiempo y aproximarla como:
Despejando la posición en el instante actual \(x_i\) obtenemos:
Con esta ecuación podemos computar la posición de la masa para el instante \(i\) si supiéramos la de los instantes anteriores.
Nota
Se pide implementar las fórmulas deducidas en este enunciado. Las mismas no son resoluciones analíticas sino numéricas.
Evolución en el tiempo
Se pide programar una función
double calcular_posicion(double xim1, double xim2, double dt, double k, double m);
que dada la posición del instante anterior xim1, la del anterior al
anterior xim2, el paso temporal dt, la constante de elasticidad
k y la masa m devuelva la posición \(x_i\) del instante
actual.
Sistema masa-resorte:
Dadas las siguientes definiciones:
#define DT 0.001
#define M 0.5
#define K 10
#define X0 10
Se pide implementar un programa que calcule la evolución del sistema masa-resorte durante 10 segundos.
Como condición inicial la masa se encuentra detenida en la posición X0
desde siempre.
El programa deberá imprimir en formato CSV las columnas \(t_i\) y \(x_i\) desde el instante inicial hasta que se alcancen los 10 segundos para cada paso temporal.
Graficación
Se pide graficar la evolución del sistema que genera el programa como salida en el software de su preferencia (planilla de cálculos, octave, gnuplot, etc.)
Validación
Se pide calcular por otro método el problema planteado (esto puede ser analíticamente, mediante otro software, con alguna calculadora online, etc.) y comparar el resultado del instante final.
Entrega
- Deberá entregarse:
El código fuente del programa desarrollado.
El gráfico de la evolución en formato JPG o PNG.
El desarrollo de la validación y una pequeña comparación con lo computado en formato TXT o PDF.
La entrega se realiza a través del sistema de entregas.
El ejercicio es de entrega individual.