Trabajo Práctico 1
Fecha de entrega: Domingo 25 de junio
Introducción
Objetivo
El objetivo del presente trabajo práctico es implementar una versión simplificada del juego Poly Bridge de simulación de puentes, realizando para ello una simulación de sistemas masa-resorte y utilizando la biblioteca gráfica SDL2.
El trabajo consiste en la resolución de un problema mediante el diseño y uso de TDAs y en la reutilización de algunos de los tipos, funciones y conceptos desarrollados a lo largo del curso en trabajos anteriores.
Alcances
Mediante el presente TP se busca que el estudiante adquiera y aplique conocimientos sobre los siguientes temas:
Encapsulamiento en TDAs,
Contenedores y tablas de búsqueda,
Punteros a funciones,
Archivos,
Modularización,
Técnicas de abstracción,
además de los temas ya evaluados en trabajos anteriores.
Nota
Este trabajo es un trabajo integrador de final de cursada. En el mismo se van a aplicar todos los temas aprendidos y además se va a evaluar el diseño de la aplicación.
Es imprescindible entender los temas de TDA y modularización antes de empezar con el trabajo.
Es imprescindible diseñar el trabajo como etapa previa a la implementación.
Cualquier abordaje que pretenda empezar a codificar sin haber ordenado el trabajo primero está condenado a fracasar contra la complejidad del problema.
Masas y resortes
En el EJ1 planteamos un problema sencillo de interacción masa-resorte donde hicimos interactuar una única masa con un único resorte, el cual tenía longitud de reposo \(l_0 = 0\). En ese problema sólo se consideraba la fuerza dada por el movimiento de la masa y la fuerza del resorte.
Vamos a complejizar este problema para por un lado tener múltiples masas y resortes, pero además para considerar longitudes de reposo diferentes a cero y además considerar la fuerza de la gravedad así como amortiguación.
En nuestro problema los resortes unen masas y la incógnita a resolver serán las posiciones de dichas masas. Estas masas arrastrarán luego en su movimiento a los resortes, los cuales no forman parte del cómputo.
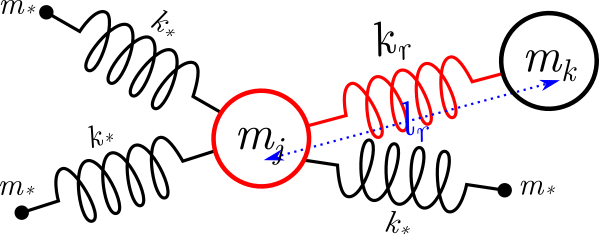
El problema analítico que queremos resolver siempre va a cumplir con la primera ley de Newton que nos dice que \(\sum \vec F = 0\), las fuerzas en este caso van a ser la fuerza producida por la inercia de la masa, pero además la fuerza de gravedad, la fuerza de los resortes y la fuerza disipativa de amortiguación. Para cada una de las masas la ecuación será algo del estilo de***:
donde \(j\) es el índice de la masa en cuestión, por lo que \(m_j\) será la masa, \(a_j\) la aceleración de esa masa y \(v_j\) la velocidad de esa masa. Esa masa estará vinculada mediante múltiples resortes \(r\) con otras masas y para cada uno de esos resortes se aplicará la ley de Hooke en la cual la diferencia entre la longitud actual \(l_r\) y la longitud de reposo \({l_0}_r\) se escalará por la constante de elasticidad de ese resorte \(k_r\). Finalmente aparecen dos constantes \(g\), la aceleración de la gravedad y \(b\) la constante de amortiguación.
(***: "del estilo de": La ecuación está escrita de forma incorrecta, no se indica qué magnitudes son vectoriales, etc., creemos que no aporta en nada recargar la notación.)
Aguantá un cacho, ¿no dijimos que la incógnita eran las posiciones?, ¡pero esa ecuación no tiene las posiciones! Sí, las tiene, \(a_j\) es la derivada segunda de la posición \(\ddot p_j\) y \(v_j\) es la derivada primera \(\dot p_j\). Ahí están las posiciones.
Notar que esta ecuación que supuestamente era para la masa \(m_j\) en realidad está vinculada con otras masas. La longitud \(l_r\), del resorte en cuestión, debe ser computada como \(\rVert p_j - p_k \rVert\) siendo \(k\) el índice de la masa del otro lado del resorte. ¡Otra vez apareció la posición!, y no sólo de esta masa, sino de las linderas. Es decir, si escribiéramos esta ecuación para cada una de las masas \(j\) tendríamos tantas ecuaciones como masas con tantas incógnitas como masas, lo que implicaría resolver un problema matricial.
Implementé el sistema matricial. Se arrastraba. Ustedes no van a pasar por eso. Por suerte no dependemos del Departamento de Matemática sino del Departamento de Computación. Simplifiquemos el problema.
Al igual que en el EJ1, vamos a resolver una solución numérica del problema, y dentro del análisis numérico hay diferentes esquemas y decisiones que pueden tomarse, algunas que pueden simplificar mucho los cálculos.
Esquema numérico
Como ya mencionamos en la sección anterior, queremos obtener las posiciones \(p_j\) para todos los nodos en cada instante. Pongámoslo explícito: las posiciones son una función del tiempo: \(p_j(t)\). No podemos resolver tiempo continuo así que vamos a discretizar el tiempo como ya lo hicimos en el EJ1.
¿Todavía no fuiste a pegarle una leída al enunciado del EJ1 para refrescar? ¿Qué estás esperando?, ¿no te pareció buena idea hacerlo cuando la tercera palabra del capítulo anterior ya lo mencionaba? ¡Andate ya mismo a repasarlo!
Entonces, el tiempo se mueve de a pasitos \(\Delta t\) y cada tiempo \(i\) lo vamos a resolver con la información de los tiempos anteriores.
Alerta de cambiamos la notación, para los tiempos en vez de usar subíndices como en el EJ1 vamos a usar supraíndices. Es decir, los tiempos serán \(t^i\), donde \(t^{i+1} = t^i + \Delta t\). (No son potencias, es notación, para no confundir con los subíndices de las masas.)
Luego cada masa \(j\) tendrá su posición para cada instante de tiempo \(i\) y la notaremos \(p_j^i\).
Primera simplificación: Tiempo discreto. ¡Check!
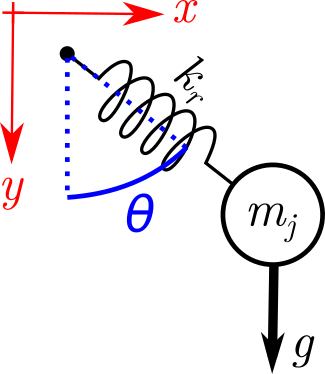
La segunda simplificación la vamos a ir a buscar al Departamento de Física. Si la fuerza de gravedad se aplica en un solo eje, metamos ejes cartesianos, matemos la ecuación vectorial (que nunca tuvo rayitas sobre los vectores), y escribamos como una operación en \(x\) y otra en \(y\).
Entonces nuestra posición \(p_j = (x_j, y_j)\) y resolveremos sobre dos ejes de forma independiente.
Nos va a quedar entonces:
Dado que las dos ecuaciones son virtualmente iguales vamos a desarrollar lo que sigue usando la de \(y\) y después escribimos las finales completas (Nota de mi yo del futuro: o no).
Estamos listo para juntar ambas simplificaciones y seguir simplificando aún más...
Ya habíamos visto en el EJ1 (¿seguís sin repasarlo?, ¿en serio?) que podíamos aproximar:
Volvamos a insistir para no perder el foco: \(y^i\) es la incógnita que no conocemos, las cosas de instantes previos son valores ya conocidos.
Antes de reemplazar y despejar ataquemos el elefante en la habitación. El término con la sumatoria vincula a cada masa con las masas linderas y genera un sistema con tantas incógnitas como masas. Es más, hay algo más fuerte que eso, hace un rato dijimos que desacoplábamos en equis y en ye y la realidad es que ese término todavía las tiene acopladas, porque para computar la longitud \(l_r\) necesito calcular la norma de un vector 2D. ¿Qué hacemos pues?
Lo que vamos a suponer es que la longitud del resorte en el instante \(i\) no va a ser muy diferente de la longitud en el instante \(i - 1\), entonces podemos reemplazar una por la otra. Que podamos reemplazar una por la otra significa que ese término pasa a ser un valor del pasado, algo conocido, una constante para la ecuación.
Ya que estamos, ¿y si nos ahorramos también los senos y cosenos? Si el coseno es la proyección del ángulo sobre el eje ye por la longitud del resorte, entonces podemos escribir:
Ahora sí, metamos en la ecuación todo: Discretización en tiempo, las expresiones numéricas de la aceleración y la velocidad y la aproximación de las longitudes y ángulos de los resortes por las del instante anterior, vamos a obtener:
(¿A vos te cuesta leerla?, yo tuve que escribirla...)
Bien, ya estamos, despejemos \(y_j^i\) que es la única variable:
Llegamos a una ecuación de tipo \(A_j y_j^i = B_j\) con \(A_j\) y \(B_j\) constantes... mmm, creo que se perdió un poco el punto: ¡¡¡Llegamos a una ecuación de tipo \(A_j y_j^i = B_j\) con \(A_j\) y \(B_j\) constantes!!! Esto quiere decir que ya no hay que resolver tantos sistemas con tantas incógnitas como masas, ahora tenemos simplemente ecuaciones con una única incógnita.
Por las dudas de que hayas hecho el CBC en pandemia, la ecuación \(A_j y_j^i = B_j\) se resuelve, aplicando álgebra muy compleja para explicarla en este párrafo, como \(y_j^i = \frac {B_j}{A_j}\).
Con eso ya está todo, numeritos que dependen de cosas que se tienen. La ecuación para las equis es idéntica cambiando las yes y tachando el término de la gravedad.
¿Qué, tampoco sabés cómo se calcula \(l_r^{i-1}\)?: Es la norma del vector \(p_j^{i-1} - p_k^{i-1}\).
Máquina de estados finita
Vamos a introducir un concepto general de modelación de problemas que consideramos que puede resultar práctico para esta aplicación.
Las máquinas de estados finitas consisten en sistemas los cuales se encuentran en un estado determinado. Mientras están en ese estado hay acciones que pueden hacer que el sistema transicione a un estado diferente.
Por ejemplo, tenemos la máquina de estados que implementa cuaquiera de los proyectores del Departamento de Computación:
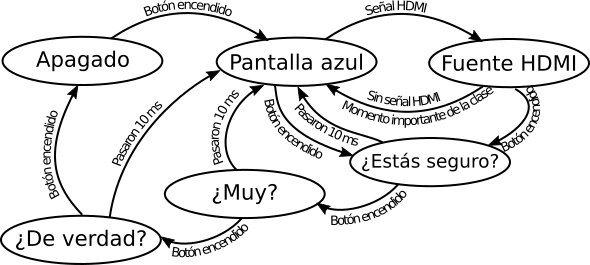
Cada uno de los óvalos representa un estado determinado. Por ejemplo, en el estado apagado, el proyector está apagado. La acción de apretar el botón de encendido (con determinada intensidad, en un ángulo determinado, una cantidad exacta de milésimas de segundo, simplifiquemos) dispara una transición al estado pantalla azul. En ese estado el proyector está prendido, proyectando una pantalla azul. Hay dos acciones que pueden sacarlo de ese estado, o la detección de la señal HDMI o que se apriete el botón de encendido. Bueno, ya se entendió.
En el lenguaje C los estados pueden modelarse con un tipo enumerativo. Mientras el tipo enumerativo permanezca en determinado valor puede ejecutarse el comportamiento que se corresponda con ese estado. Luego, puede haber eventos dentro del programa que dependiendo del estado actual modifican ese enumerativo al estado siguiente.
SDL2 en 5 minutos
Para la representación gráfica se utilizará la biblioteca gráfica SDL2.
Una aplicación gráfica tiene un pseudocódigo más o menos de este estilo:
main() {
inicializar;
while(1) {
leer la entrada del usuario;
procesar lo que haya que procesar;
dibujar la pantalla;
esperar un ratito para cumplir con los FPS;
}
destruir;
}
Se provee un esqueleto completo con esta lógica, donde se indica dónde el alumno tiene que completar con su código. De SDL2 sólo habrá que aprender a leer el mouse, a dibujar líneas y cuadrados y a cambiar el color. El resto ya está hecho.
Se proveen ejemplos tanto de mouse, como del dibujado de cosas.
Las coordenadas del mouse SDL2 las informa en píxeles desde la esquina superior izquierda de la pantalla. Convenientemente los ejes tienen la misma orientación que usamos cuando descompusimos nuestras ecuaciones, ¿será casualidad?
Ahora bien, la pantalla tiene 800 pixeles y simular esos 800 pixeles como si fueran 800 metros sería muy lento por la escala de tiempo. Entonces para convertir entre las coordenadas en pixeles de la pantalla a las longitudes en metros de la malla vamos a dividirlas por 50. Es decir, 1 pixel de pantalla va a representar 2 cm en la malla.
Al convertir del mouse a la malla habrá que dividir por 50 y al querer mostrar cosas de la malla en la pantalla habrá que multiplicar por 50.
Distancia de un punto a un segmento de recta
Para determinar la distancia de un punto \(p = (x_p, y_p)\) a un segmento de recta \(\overline{p_j p_k}\) dado por dos puntos \(p_j = (x_j, y_j)\) y \(p_k = (x_k, y_k)\), y asumiendo que la longitud de \(\overline{p_j p_k}\) es distinta de cero, puede computarse:
Si el parámetro \(\alpha \leq 0\) entonces el punto del segmento más cercano a \(p\) es el punto \(p_j\), si \(\alpha \geq 1\) el punto más cercano será \(p_k\), y en el caso de que \(0 < \alpha < 1\) el punto más cercano estará dado por \(p_j + \alpha \left( p_k - p_j \right)\).
Sabiendo cuál es el punto del segmento más cercano a \(p\) se puede calcular la distancia entre ambos puntos que será la distancia del punto a la recta.
El juego
Se desea realizar un juego con dos etapas diferenciadas: La primera de ellas consiste en la construcción gráfica de la malla a utilizar, la segunda consiste en simular esta red y verificar si cumple las pautas de deformación máxima.
Malla
Durante la etapa de la construcción se debe interactuar con la malla, entonces previo a entrar en la dinámica hablemos de la malla.
La malla debe permitir garantizar las restricciones del juego y funcionar de forma más o menos eficiente para determinadas operaciones.
Las restricciones y operaciones son:
Ningún resorte puede ser mayor a determinada longitud fija.
Se debe poder buscar una masa dada una posición, la búsqueda será dentro de un radio con respecto a la posición.
Se debe poder buscar un resorte dada una posición, la búsqueda será dentro de un radio con respecto a esa posición.
Tanto los resortes como las masas tienen que poder ser eliminados. Ahora bien eliminar una masa implica que deben ser eliminados los resortes que la referencian.
Las masas tienen que poder ser movidas. Ahora bien, siempre y cuando ese movimiento no rompa la longitud máxima. Pero, también hay masas que son fijas. Esas no pueden ser movidas.
Al menos los resortes tienen que estar contenidos en una lista enlazada. Notar que los resortes sencillamente se recorren para todas las operaciones, por lo que no hay un orden ni acceso por índice.
Vamos un poco al diseño.
Como ya se sabe, este trabajo es sobre TDAs. Deben ser TDAs tanto los resortes, como las masas, como la malla.
El usuario Bárbara que utilice la malla puede conocer a los TDAs de los resortes y las masas. Es decir, tranquilamente una primitiva de búsqueda sobre la malla puede devolver el resorte o el nodo que corresponda.
Hay una operación recurrente que necesita ser resuelta en tiempo constante y es el recuperar las masas (y por ende sus coordenadas) asociadas a un resorte. (¿Por qué recurrente?, mirar las ecuaciones ya desarrolladas, todo el tiempo necesitamos aplicar a cada resorte sobre sus respectivos nodos u obtener la longitud de un resorte dado.)
Esto plantea un problema con múltiples soluciones, y termina siendo trasnversal al diseño de los tres TDAs. ¿El resorte guarda índices de masas?, ¿el resorte guarda punteros a las masas?, ¿las masas guardan su índice?, ¿pero si las masas guardan su índice entonces conocen de la existencia de la malla?, ¿las masas tienen índices?, ¿la malla no debería ser de más alto nivel que las masas?... ¿se entiende las preguntas? Son preguntas abiertas y son las preguntas que uno debería hacerse cuando diseña cualquier tipo del problema.
No hay una solución correcta. Hay criterios. Y los criterios tienen que estar debidamente justificados en la documentación de los TDAs. Un criterio puede estar mejor o peor, pero un TDA que no explicite los criterios está siempre mal, porque sin conocer qué se quiso resolver y por qué no se puede saber si la implementación es correcta.
Fase de construcción
Durante la fase de construcción el usuario tiene que poder crear una malla de forma interactiva.
A qué nos referimos con:
Clickear: El usuario aprieta un botón del mouse y lo suelta en el mismo lugar.
Arrastrar: El usuario aprieta un botón y sin soltar el mouse lo mueve, soltando el mouse en algún otro lugar.
Deben implementarse el siguiente comportamiento:
Si se clickea sobre un lugar vacío se agrega una masa en ese lugar.
Si se arrastra desde la posición de una masa se intenta mover dicha masa al lugar donde termine el arrastre.
Si se clickea sobre una masa existente entonces se inicia el dibujado de un nuevo resorte que va a ir desde ese nodo hasta donde se haga click para finalizar. Si en el lugar de finalización hay una masa existente, el resorte va a ir de una masa a la otra, si no, se agregará una masa nueva.
Si se hace click derecho sobre una masa, la misma se borra. A menos que sea una masa fija, esas no se pueden borrar.
Si se hace click derecho sobre un resorte, el mismo se borra.
Notar que SDL informa de la acción de apretar el botón, mover el mouse o soltar el botón como eventos sueltos. Los conceptos de click y arrastre deben ser construidos en base a estos eventos de bajo nivel.
Fase de simulación
Durante la fase de simulación se toma la malla generada en la fase de construcción pero no es necesario utilizar la estructura malla si no que puede generarse algún tipo de estructura adicional.
La simulación debe estar encapsulada en un TDA. A dicho TDA tiene que poder pedírsele que itere un \(\Delta t\) adicional y debe ser capaz de realizar esta operación.
Volviendo a la resolución del problema, el problema es similar al EJ1. En el EJ1 se guardan dos valores previos y esos valores se utilizan para calcular el instante actual. En el nuevo problema no hay una masa sino múltiples, por lo que hay que guardar dos valores en el pasado para cada una de ellas. Y además el problema es bidimensional, por lo que cada masa tiene dos valores. Para almacenar estos valores es necesario almacenar las posiciones de cada masa en dos instantes. Para esto pueden usarse matrices de \(n\times2\). Alcanza con solo almacenar dos instantes, con el \(\Delta t\) que se está utilizando sería imposible almacenar todos los pasos de cómputo.
Para resolver el problema hace falta computar los términos \(A_j\) y \(B_j\) ya mencionados para cada una de las masas. Esta operación se va a realizar en dos partes:
Para cada masa, se computan los términos de \(A_j\) y \(B_j\) que dependen de las masas.
El término de la gravedad debe suprimirse tanto en los términos en el eje equis, como en los términos donde la masa sea fija. Las masas fijas no están afectadas por la gravedad.
Para cada resorte, se computan los términos de \(B\) que dependen del resorte. Notar que al iterar cada uno de los resortes \(r\) este resorte va a señalar a dos masas y va a modificar entonces tanto a \(B_j\) como a \(B_k\). Según cuál de los dos sea, el término que resta las dos posiciones y aproxima el seno/coseno cambia de signo.
Si el nodo \(j\) fuera fijo no se sumaría ese término en \(B_j\) y si lo fuera \(k\) se debe proceder del mismo modo.
Una vez se tenga el vector \(A\) y \(B\) armados puede resolverse el sistema.
Un par de observaciones:
En el ciclo sobre los resortes, dado un resorte \(r\) hay que vincularlo con los índices de sus masas porque en esa posición hay que aplicar la operación. Releer la discusión que se propone en el TDA de la malla.
De alguna forma, cuando se entra en la fase de simulación esta operación debe ser resuelta en tiempo constante. Como se dice al inicio de esta sección, el TDA que realiza la simulación puede o no utilizar a la malla original, bien puede hacer algún tipo de copia que ponga índices fijos y conocidos. O no. Es decisión de diseño pero sea como sea tiene que poder garantizarse la recuperación eficiente de las masas de un resorte.
Se propuso un algoritmo que "resuelve" las nuevas coordenadas de todas las masas, incluídas las masas fijas... ¿pero no es que las masas fijas no se movían? Bueno, si mirás las ecuaciones y te fijás las aclaraciones que se hicieron cuando se explicó la metodología de cálculo si a las masas fijas no se le aplica ni la gravedad ni tampoco se le aplica la fuerza del resorte, las ecuaciones se compensan y la masa debería quedar fija, salvo errores numéricos.
En el caso de que los errores numéricos sean realmente errores numéricos (y no que se implementaron mal las ecuaciones) puede hacerse un postproceso para forzar a que las coordenadas de las masas fijas queden en su lugar.
También se puede replantear el algoritmo propuesto para directamente excluir del cómputo a las masas fijas... pero eso implica renumerar y tener casos particulares en los resortes que parecen más complicados que lo que se propuso.
La simulación debe ejecutarse en tiempo real. Es decir, si la aplicación se refresca a una determinada cantidad de FPS, se deben hacer tantas iteraciones de simulación como sean necesarias para avanzar de a un \(\Delta t\) por vez el tiempo necesario para equiparar el tiempo del dibujado. Tiempo real significa eso: El tiempo de la simulación es la misma que el tiempo en la vida real.
De una fase a la otra
A la simulación se entra haciendo click derecho sobre un lugar donde no haya una masa o un resorte.
Al momento de entrar a la simulación las longitudes en reposo de los resortes tienen que ser las dadas por las coordenadas de sus masas. Si estas longitudes no se computaron al manipularlos, bien puede hacerse ese cómputo en ese momento.
El \(k\) de cada resorte se computa como \(\frac{k_b}{(l_0)^p}\) con \(k_b\) y \(p\) parámetros de configuración.
La suma de todas las masas tiene que ser de una magnitud dada, pesando todas las masas el mismo valor.
Esto era un juego, ¿no?
El juego consiste en diferentes "niveles".
Cada nivel empieza con dos masas fijas. En el primer nivel estas masas estarán a una distancia horizontal de 4 unidades entre una y la otra. Cada vez que se gane un nivel se empezará con una nueva malla, con una unidad más de distancia que el nivel anterior.
La simulación se animará en pantalla durante 10 segundos.
Al concluir esos 10 segundos se computará el porcentaje de estiramiento de cada resorte según \(\frac{l - l_0}{l_0}\), si ese número llegara a ser mayor al máximo admitido para algún resorte entonces no se gana el nivel y se vuelve a la fase de construcción con la malla previa a la simulación.
En caso de que ningún resorte supere el umbral entonces se limpiará la malla y se iniciará un nuevo nivel, como se dijo, con los nodos fijos más alejados entre sí.
Para que sea un juego, tenemos que poder competir, ¿no? El puntaje se computará como la cantidad de resortes necesarios para pasar un nivel. Claramente menos puntos implica una mejor resolución.
¿Y cómo le muestro al mundo lo buena que fue mi resolución de un nivel? Al
ganar cada nivel debe escribirse un archivo binario nivel_#.bin con la malla
ganadora.
¿Y para qué me sirve ese binario?, si el programa se ejecuta recibiendo un archivo como parámetro, deberá simular esa malla.
¿Qué pasa si el usuario se aviva de que nuestro programa no se da cuenta de si realmente la malla une los dos nodos fijos?, cursá Algoritmos y Programación 2 el cuatrimestre que viene y después arreglalo. Todo no se puede.
Trabajo
Ya se dijo todo lo que había por decir.
El problema que se plantea en este trabajo deberá ser resuelto con las herrramientas ya adquiridas, extendiendo de forma consistente los TDAs ya planteados de ser necesario y diseñando los TDAs nuevos que hagan falta. Se evaluará además el correcto uso de los TDAs respetando la abstracción y el "modelo" de Alan-Bárbara, así como la separación de los cómputos físicos con respecto a la lógica de representación gráfica.
Se pide diseñar una aplicación que pueda ser ejecutada como:
$ ./monobridge <archivo.bin>
que permita jugar al juego que describimos con toda la lógica que se mencionó. El archivo es opcional, en caso de recibirlo se procederá como ya se explicó.
Se deben implementar TDAs donde se considere que es necesario.
Al menos los Resortes, Masas, Malla y Simulador tienen que ser implementados como TDAs con sus características y comportamiento.
El alcance es lo especificado en este enunciado. En cualquier aplicación amplia como esta siempre pueden implementarse detalles adicionales, los mismos no forman parte del enunciado y no hay que hacer nada adicional para alcanzar la máxima nota. La prioridad es resolver completa la funcionalidad descrita para terminar con eso la materia.
Material
Fuentes
En la sección de Material del sitio web está la lista enlazada que debe usarse, sin modificaciones de ningún tipo, para (al menos) almacenar los resortes.
Se provee además el ejemplo de SDL2, el cual tiene todas las constantes que se
mencionaron de forma genérica en este enunciado, disponible para descargar en:
archivos_20231_tp1.tar.gz
Valgrind
En el caso de una aplicación construída con SDL2 se hace complejo el uso de Valgrind porque esta biblioteca tiene desprolijidades en su implementación que hacen que Valgrind tire múltiples errores y estos errores a la tasa que marquen los FPS del juego. Por eso para poder testear con Valgrind sobre el código desarrollado tenemos que suprimir los errores que son relativos a SDL2.
Se provee el siguiente archivo de supresiones para Valgrind:
suppressions_20231_tp1.supp
Con este archivo descargado Valgrind puede ser invocado como:
$ valgrind --suppressions=suppressions_20231_tp1.supp --leak-check=full ./monobridge
con lo que el programa se ejecutará suprimiendo los millones de errores de SDL2.
Al haber errores y haberlos suprimido el reporte no será del todo satisfactorio, y va a haber memoria en el heap y elementos marcados como "still reachable". El siguiente es un reporte de ejemplo:
==27213== Memcheck, a memory error detector
==27213== Copyright (C) 2002-2017, and GNU GPL'd, by Julian Seward et al.
==27213== Using Valgrind-3.13.0 and LibVEX; rerun with -h for copyright info
==27213== Command: ./hangon
==27213==
==27213==
==27213== HEAP SUMMARY:
==27213== in use at exit: 196,326 bytes in 1,058 blocks
==27213== total heap usage: 32,817 allocs, 31,759 frees, 118,233,488 bytes allocated
==27213==
==27213== LEAK SUMMARY:
==27213== definitely lost: 0 bytes in 0 blocks
==27213== indirectly lost: 0 bytes in 0 blocks
==27213== possibly lost: 0 bytes in 0 blocks
==27213== still reachable: 2,037 bytes in 10 blocks
==27213== suppressed: 194,289 bytes in 1,048 blocks
==27213== Reachable blocks (those to which a pointer was found) are not shown.
==27213== To see them, rerun with: --leak-check=full --show-leak-kinds=all
==27213==
==27213== For counts of detected and suppressed errors, rerun with: -v
==27213== ERROR SUMMARY: 0 errors from 0 contexts (suppressed: 1018824 from 25)
Notar que pese a que se señala más de un millón de errores, el reporte de
pérdidas dice que no hay bloques ni definitiva, ni indirecta ni posiblemente
perdidos. Además el reporte, pese a haber sido corrido con --leak-check=full
no muestra ningún error en nuestro propio código.
Se busca que el reporte tenga estas características.
Ahora bien, prestar atención porque ignorar los errores de still reachable
puede enmascarar errores como por ejemplo no haber llamado a fclose() entre
otros.
Nota
Ejecutar con Valgrind implica a poner a un programa a analizar cada cosa que hace nuestro programa. Con un programa pesado en cantidad de operaciones como el nuestro, el programa va a andar muy lento.
La idea es correr con Valgrind como un chequeo a realizar, pero no todo el tiempo durante del desarrollo.
Para liberar la carga, sólo durante las corridas de Valgrind, se puede
reducir el valor de JUEGO_FPS a un valor que lo haga más manejable. Esto
va a alterar un poco la fluidez del juego. También se puede modificar el
\(\Delta t\)), lo cual va a arruinar la simulación, pero igual sirve
para testear intensivamente la memoria.
Funcionamiento
Tal vez les suba después un videito de mi implementación para que vean comportamiento, pero pueden mirarlo de cuando presenté el trabajo en clase.
Entrega
Requisitos
Los únicos requisitos son que el programa resuelva correctamente la funcionalidad pedida y que lo haga utilizando TDAs con un diseño planificado a conciencia. Si hacés eso nada puede salir mal.
Entregables
Deberá entregarse:
El código fuente del trabajo debidamente documentado.
El archivo
Makefilepara compilar el proyecto.
Nota
El programa debe:
estar programado en C,
estar completo,
compilar...
sin errores...
sin warnings,
correr...
sin romperse...
sin fugar memoria...
resolviendo el problema pedido...
Trabajos que no cumplan con lo anterior no serán corregidos.
La entrega se realiza a través del sistema de entregas.
El ejercicio es grupal permitiéndose grupos de hasta 2 integrantes.
Si elegís hacer el trabajo en grupo te pedimos que nos avises o por mail o por Discord quién es tu compañero de grupo así lo cargamos en el sistema de entregas. (Si el grupo sufriera alteraciones avisanos también.)