Ejercicio obligatorio 2

Fecha de entrega: Lunes 18 de septiembre

Introducción

Polilíneas de Bézier

Una curva de Bézier de grado \(n\) 2D se construye en base a \(n + 1\) puntos de control, donde cada uno de estos puntos es una coordenada \((x, y)\). La curva de Bézier pasa por el primero y último punto, mientras que los demás determinan la curvatura.

Para hacer figuras complejas pueden usarse múltiples curvas de Bézier consecutivas. Como se quiere que la curva sea continua, cada curva debe empezar donde terminó la anterior, y dado que las curvas pasan por los puntos extremos esto implica que cada curva comparten su primer y útimo punto...

Ejemplo, si se tienen curvas de Bézier de grado 2, entonces cada una de ellas se forma con 3 puntos. Ahora bien, si se quiere una sucesión de curvas que use como puntos de control los puntos: A, B, C, D, E, F, G se pueden empalmar 3 curvas: ABC, CDE, EFG:

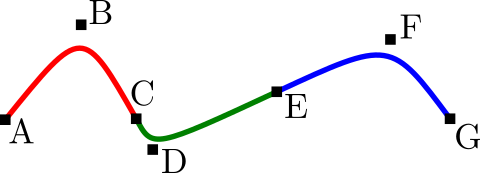
Entonces dado que una polilínea se forma con \(m\) puntos de control y cada punto de control pertenece a \(\mathbb R^2\), la misma puede modelarse en el lenguaje de programación C como una matriz float [M][2].

Notar que para curvas de Bézier de grado \(n\), se verifica que \(m = k n + 1\), donde \(k\) será el número de segmentos. En el ejemplo anterior teníamos 3 segmentos y el grado era 2, y se verifica que el número de puntos era 7.

Implementación

Traslación de puntos

Se pide implementar una función void trasladar(float puntos[][2], size_t m, float dx, float dy); que, dado un vector puntos con m puntos y el formato ya descrito modifique cada una de sus componentes mediante la adición del par (dx, dy).

Rotación de puntos

Se pide implementar una función void rotar(float puntos[][2], size_t m, double rad); que dado un vector de puntos rote cada uno de ellos rad radianes con respecto al origen de coordenadas.

Nota

Recordar que para rotar un par de coordenadas \((x, y)\) un ángulo \(\theta\) se debe realizar la operación:

\(\begin{bmatrix}x' \\y' \\\end{bmatrix} = \begin{bmatrix}\cos \theta & -\sin \theta \\\sin \theta & \cos \theta \\\end{bmatrix}\begin{bmatrix}x \\y \\\end{bmatrix}\).

La operación puede descomponerse como:

\(x' = x \cos \theta - y \sin \theta\),

\(y' = x \sin \theta + y \cos \theta\).

Cercanía de punto a curva de Bézier

Se pide implementar una función double cercania_a_bezier(int n, float puntos[n + 1][2], float px, float py); que dada la curva de Bézier de grado \(n\) dada por los puntos devuelva el valor de \(t\) en el que hay que evaluar a dicha curva para que esté lo más cercana del punto \((px, py)\).

Dado que no hay una expresión explícita de la distancia mínima entre la curva y el punto, operativamente hay que evaluar puntos en la curva y determinar cuál de ellos minimiza la distancia al punto dado.

Nota

Es recomendable construir funciones auxiliares para realizar este proceso.

Bézier 1D

Se pide implementar una función double bezier(int n, float c[n + 1], double t); que devuelva la evaluación de una curva de Bézier de grado n para c coordenadas 1D, es decir calcula y devuelve \(\sum_{i=0}^n c_i B_i^n(t)\).

Aplicación

Teniendo los siguientes puntos de control:

float puntos[][2] = {
        {0.17305465, 10.136934},
        {0.19149611, 23.287691},
        {12.230908, 23.62676},
        {15.632344, 15.423703},
        {15.632344, 15.423703},
        {13.223768, 15.479423},
        {13.223768, 15.479423},
        {7.7396987, 22.246678},
        {2.9096797, 16.657932},
        {2.7566421, 10.345005},
        {2.6054406, 4.1079585},
        {8.3739896, -0.49167977},
        {13.273927, 5.6239999},
        {13.273927, 5.6239999},
        {16.023752, 5.5849339},
        {16.023752, 5.5849339},
        {13.505533, -1.4803139},
        {0.15461584, -3.0138257},
        {0.17305465, 10.136934},
};

que corresponden a una curva de Bézier de grado 3, escribir una aplicación que rote estos puntos, los desplace y luego "dibuje" la curva en formato CSV. Los puntos de control generan una letra C.

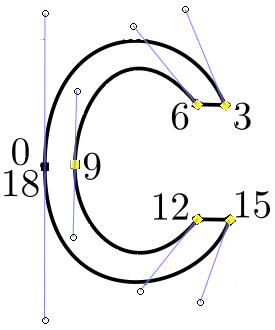
Testear además el funcionamiento de la función cercania_a_bezier() para alguno de los segmentos y validar visualmente que funcione correctamente.

Entrega

Deberá entregarse el código fuente del programa desarrollado.

El programa debe compilar correctamente con los flags:

-Wall -Werror -std=c99 -pedantic

y validar los ejemplos dados.

La entrega se realiza a través del sistema de entregas.

El ejercicio es de entrega individual.