Ejercicio obligatorio 1
Fecha de entrega: Lunes 23 de septiembre
Introducción
Las redes neuronales son el corazón de los sistemas de inteligencia artificial.
Una red neuronal está conformada por neuronas, que se interconectan entre sí. Las neuronas se excitan con los estímulos que reciben y se activan con determinados estímulos.
Las redes neuronales se estructuran por capas, hay una primera capa que es excitada por las señales de entrada, que propaga su información a la siguiente capa, esta a la siguiente y así hasta llegar a la última capa que es la capa de salida.
En el siguiente diagrama:
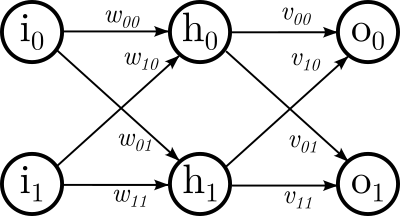
Tenemos una capa de entrada con dos neuronas \(i_0\) e \(i_1\), una segunda capa con dos neuronas \(h\) y, por último, una capa de salida también con dos neuronas \(o_0\). En este modelo la entrada serían dos valores al igual que la salida. En una red neuronal podemos tener tantas entradas, tantas salidas, tantas capas intemedias y la cantidad de neuronas en cada capa intermedia que queramos.
Las flechas representan las conexiones, todas las neuronas de una capa están comunicadas con todas las neuronas de la capa siguiente. Estas conexiones se representan como pesos que denotan el grado de conexión. Los pesos son números reales.
Si queremos calcular la excitación de determinada neurona tenemos que computar el aporte de cada una de las conexiones entrantes.
Por ejemplo, si tuviéramos una determinada entrada \(i_0\) e \(i_1\) y quisiéramos calcular la excitación de la neurona \(h_0\) deberíamos sumar la contribución de la entrada según los pesos de las conexiones:
Análogamente podemos calcular el aporte de cada una de las demás neuronas siguiendo este esquema.
Notar que si:
y \(I = \left( i_0, i_1 \right)\) y \(H = \left( h_0, h_1, h_2 \right)\) entonces podemos ver que:
el producto matricial de dos matrices.
Es más, en principio \(O = I W V\), obtenemos la salida de nuestra red simplemente multiplicando las matrices que representan los pesos.
Si bien esta es la idea general ahora vamos a complejizar un poquito más este modelo.
En primer lugar vamos a agregar un factor que se llama bias, que simplemente es un número que se suma o resta en nuestra neurona:
no viene al caso explicar qué representa este valor, pero sirve para que la red funcione. Si bien estamos adosando este valor por fuera de la operación matricial es fácil incluir al mismo en ella.
Si nuestra entrada tiene una determinada cantidad de neuronas, agregaremos una entrada adicional que valdrá siempre 1. En nuestro ejemplo entonces \(I = \left(i_0, i_1, 1 \right)\). Y eso generará nuevas conexiones y agregará una nueva fila en la matriz \(W\), bueno, \(b_0\) es básicamente la primera columna de esta última fila:
En segundo lugar la física de las neuronas es más compleja. Si consideráramos que el resultado de \(IW\) es el valor de las neuronas de \(H\) diríamos que las funciones se activan de forma lineal. En la vida real las neuronas se saturan, es decir, hay un umbral en el que reaccionan pero si la excitación es demasiada no se excitan proporcional a ella. Para tener una analogía pensemos en la sensación de dolor, dentro de determinado umbral el dolor que sentimos es proporcional a lo que produce el dolor, ahora bien, pasado determinado punto alcanzamos un máximo y no importa ya la intensidad del estímulo.
Lo que vamos a hacer es aplicar una función de activación al resultado de nuestra cuenta. Hay múltiples funciones pero elijamos la función sigmoidea logística:
Que tiene la siguiente gráfica:
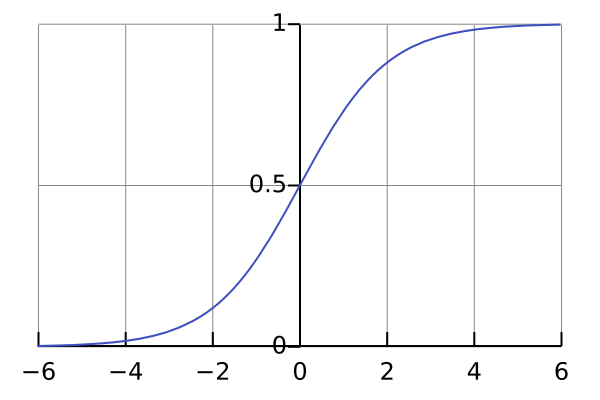
Notar que la activación se mantiene estable entre 0 y 1, sin importar lo extremo de la excitación.
Entonces cuando operemos \(IW\) esa será la excitación de las neuronas de \(H\) pero tendremos que aplicarle \(\sigma(x)\) a cada uno de esos valores para obtener la activación de las neuronas.
Por ejemplo, para calcular el valor de \(h_0\) que habíamos computado antes sin la función de activación sería:
Si asumimos que agregamos un 1 a la entrada podemos decir que:
(Cuando notamos \(\sigma(X)\) con \(X\) algo multidimensional queremos decir, aplicarle \(\sigma(x)\) a cada elemento \(x_i\).)
Entonces, la salida completa será \(O = \sigma(\sigma(IW)V)\), una composición de productos matriciales y funciones de activación.
Entrenamiento
Hasta ahí el modelo. Bien. Si tuviéramos las matrices de pesos podríamos computar la red neuronal que quisiéramos. ¿Pero cómo hacemos para generar esos pesos en primer lugar?
Bueno, los modelos neuronales siempre se construyen en base a un juego de datos de entrenamiento. En el juego de datos de entrenamiento sabemos tanto la entrada como la salida para determinados casos. Si entrenamos bien nuestra red, entonces la red debería poder reaccionar tanto a datos del entrenamiento como a datos nuevos (si los datos de entrenamiento fueran representativos).
El procedimiento para entrenar una red es el siguiente: Se empieza con pesos aleatorios, generalmente entre 0 y 1.
Luego se excita la red según alguno de los casos de entrenamiento. Esto nos dará una salida, que probablemente esté muy mal, dado que la red no está entrenada.
Lo que vamos a hacer es computar el error, o sea, qué tan mal está la salida que tuvimos con respecto a la deseada.
Generalmente se utiliza de métrica el error cuadrático. Si suponemos que \(\hat O\) es el valor esperado y \(O\) es el resultado de nuestra red:
La idea es utilizar ese error para decidir qué coeficientes ajustar para distribuir ese error entre los diferentes pesos y de esa manera mejorar la predicción. El algoritmo más común para realizar esta operación se llama backpropagation.
Este proceso es un proceso iterativo, se realiza para cada uno de los valores de entrenamiento no una si no muchas veces. Si el entrenamiento fue adecuado (y la geometría de nuestra red es buena para el problema) al final tendremos una red con pesos razonables que será capaz de predecir salidas a entradas.
Recapitulación
El modelo que presentamos para cada una de las neuronas es lo que se llama un perceptrón simple.
Si bien en nuestro esquema inicial presentamos la red en su conjunto, después de todas las adiciones que hicimos el modelo de cada una de las neuronas nos quedó así:
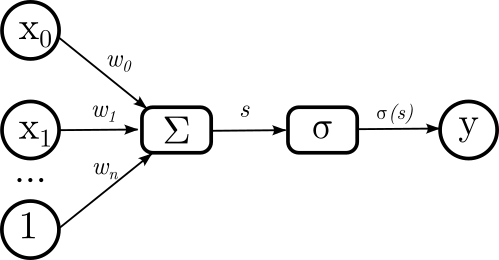
Es decir, para computar la salida de nuestra neurona \(y\) pasamos por diferentes estadíos. Primero entran las señales de cada una de las neuronas de la capa anterior \(x_i\) más el bias 1. Esos valores se multiplican por los pesos relativos dados por \(w_i\) y se suman. Eso genera el estímulo \(s\). Ahora bien, este estímulo se pasa a través de la función de activación \(\sigma\) y es este el valor final de mi neurona.
Reiteramos:
No dijimos nada nuevo, sólo remarcamos que la salida viene de la función de activación, que a su vez viene de una sumatoria, que a su vez viene de aportes individuales de las neuronas previas por sus respectivos pesos. Lo vamos a utilizar en la próxima sección.
Backpropagation
Como ya se dijo, la forma más usual de entrenar redes es con el algoritmo de backpropagation.
En este algoritmo vamos a computar la actualización de cada peso \(w_i\) (y \(v_i\)) individual de nuestras matrices como \(\frac{\partial L}{\partial w_i}\).
Recordemos la regla de la cadena que nos decía que si \(y = f(u)\) y \(u = g(x)\) podemos escribir:
En nuestro método la derivada buscada la resolveremos según la cadena de sus diferentes componentes... porque no nos olvidemos de que nuestra salida no es otra cosa que una concatenación de funciones.
Antes de ir a las cuentas notar que:
Empecemos, por ejemplo, con el cómputo en la capa \(V\), supongamos el peso dado por \(v_{00}\), calcularemos la contribución del error \(L\) a \(v_{00}\) según:
Recordemos el concepto de derivada parcial: Nuestra variable de derivación es \(v_{00}\), por lo que todos los términos que no dependan de ella van a ser derivados como si se tratara de constantes y nada más.
\(L\) era el error y contenía el valor de la salida, que ya sabemos que es una combinación lineal de muchas cosas... ahora bien, sólo \(o_0\) depende de \(v_{00}\). De este modo podemos aplicar la regla de la cadena en el sentido que nos interesa:
Y parece un choclazo pero vamos a ver que la operatoria es sencilla, para que se entienda por dónde viene la mano por ejemplo: si tenemos una sumatoria donde cada término está afectado por un único peso entonces sólo va a sobrevivir el término de \(v_{00}\).
Vayamos por partes, ataquemos la primera derivada:
¿Toda esa línea termina en eso? Sí, fijate que de la sumatoria el término de \(o_1\) no importa y entonces es sólo derivar \(\frac12\left(\hat o_0 - o_0\right)^2\) con respecto a \(o_0\).
El siguiente término de nuestra derivada es la derivada de la salida con respecto a la sumatorial. En el perceptrón este término es el que aplica la función de activación, y ya vimos la derivada de esta función. Por lo tanto:
Y finalmente el último término, tenemos la derivada de \(h_0 v_{00} + h_1 v_{10} + 1 v_{20}\):
Entonces poniendo todo junto:
Todos los parámetros que aparecen son términos que tuvimos que calcular cuando computamos la salida. Esto es apenas una cuenta sencilla.
Habiendo computado este término calcularemos el nuevo valor \(v_{00}'\) como:
donde el parámetro \(\eta\) es el grado de aprendizaje. Cuando empecemos a entrenar este valor será alto, porque queremos moldear mucho la red e iremos descendiendo su valor a medida que queramos hacer ajustes más finos.
Notar que el peso \(v_{00}\) es el que relaciona a \(h_0\) con \(o_0\), genéricamente \(v_{ij}\) relaciona a \(h_i\) con \(v_j\). Luego, para todos los pesos de \(V\) podemos escribir:
Si te perdiste, esta última fórmula y la anterior son las únicas dos que van a importarnos cuando actualicemos las matrices, el resto fue el desarrollo para llegar acá.
Si vamos a los pesos de la matriz \(W\) podemos seguir un enfoque similar. Ahora bien, observemos una diferencia importante entre las dos capas de neuronas con respecto a la salida. En la última capa cada peso incide en un solo valor de la salida, en cambio en la primera capa cada neurona incide en los pesos de la salida. Como \(L\) es una sumatoria de tantos términos como salida, computemos por separado cada una de ellas y después sumemos al final. Entonces:
Dado que es una cadena, los primeros términos son los mismos que ya computamos para la capa de salida. Veamos los nuevos:
(Es la misma derivada que antes pero ahora derivamos en función de \(h_0\)).
Análogamente a antes, cuando derivemos la función de activación:
Y finalmente no debería ser sorpresa que el último término sea:
Entonces:
No nos olvidemos que:
es decir, habíamos partido la sumatoria en 2. Otra vez, si suponemos un \(w_{ij}\) entonces:
Esta última es la otra ecuación importante.
No nos olvidemos de que teniendo el aporte del error al peso entonces vamos a actualizar según:
¿Hacemos un ejemplo?
Imaginemos que queremos entrenar una red de dos entradas y dos salidas con un único caso de entrenamiento:
Así se vería la red (en verde los datos de entrada, en rojo los que calcularemos):
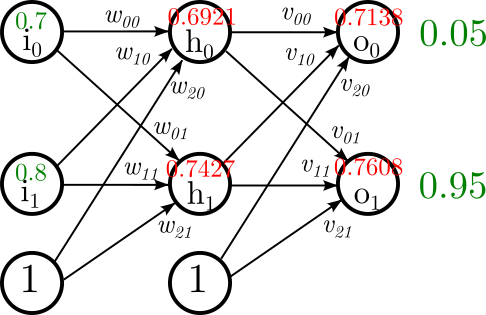
Ahora bien, empezamos nuestro problema con los siguientes valores:
Computemos:
Análogamente \(h_1 = \sigma(1.06) = 0.7427\).
Acabamos de computar \(H = \sigma((0.7, 0.8, 1) W) = (0.6921, 0.7427)\).
Computemos ahora:
Análogamente \(o_1 = \sigma(1.157) = 0.7608\).
Acabamos de computar \(O = \sigma(\sigma((0.7, 0.8, 1) W) V) = (0.7138, 0.7608)\).
Ahora bien, nosotros esperábamos que la salida fuera \((0.05, 0.95)\), ¿está bien computado esto? Sí, está bien computado... pero entendamos que estamos partiendo de una red no entrenada. Tenemos un montón de error, particularmente tenemos:
Lo siguiente sería entrenar a la red para que mejore en su predicción.
Empecemos por \(v_{00}\):
Análogamente para los otros valores:
Ataquemos ahora \(w_{00}\):
(Omitimos recalcular los números que ya precalculamos.)
Luego:
Entonces:
Totalizando:
Ahora ya tenemos todo lo necesario como para entrenar nuestra red.
Debemos computar la actualización, para eso vamos a elegir \(\eta = 0.5\):
Entonces tenemos
Esa será la nueva \(W\).
Y análogamente:
Si volviéramos a correr el problema con estos nuevos valores ahora la salida sería \(O = (0.6847, 0.7670)\) y el error bajaría un 10% a \(L = 0.218191\).
Manteniendo el mismo \(\eta\) en 100 iteraciones obtenemos \(O = (0.1012, 0.9083)\) y en 1000 iteraciones \(O = (0.05137, 0.9487)\).
En un entrenamiento real no entrenaríamos a la red siempre con el mismo caso si no que alternaríamos entre todos nuestros casos de entrenamiento. La idea de una red es que nos sirva para clasificar casos conocidos e interpolar casos nuevos, por eso es que las entrenaremos con casos diferentes.
Trabajo
Función sigmoidea logística
Implementar una función double sigmoidea(double x) que dado un x
devuelva la evaluación de la función sigmoidea logística en x.
Imprimir matrices
Implementar una función void imprimir_matriz(size_t fs, size_t cs, float m[fs][cs]);
que imprima los elementos de la matriz m por stdout.
Inicializar matrices
Implementar una función void inicializar_matriz(size_t fs, size_t cs, float m[fs][cs]);
que inicialice la matriz m en valores aleatorios entre 0 y 1.
Extraer fila
Implementar una función void extraer_fila(size_t cs, float origen[][cs], float destino[cs], size_t fila);
que extraiga la fila indicada del la matriz origen y la guarde en el vector destino.
Extender vector
Implementar una función void extender_vector(size_t n, const float origen[n], float destino[n + 1]);
que copie los elementos de origen a destino e inicialice en 1 el valor que sobra en destino.
Aplicar función
Implementar una función void aplicar_funcion(size_t n, float v[n]); que
aplique la función sigmoidea logística a cada uno de los elementos del vector v.
Actualizar matriz
Implementar una función void actualizar_matriz(size_t fs, size_t cs, float m[fs][cs], float l[fs][cs], float eta)
que aplique actualice m en base a l y eta según \(M' = M - \eta L\).
Multiplicar
Implementar una función void multiplicar(size_t nx, size_t ny, const float x[nx], float w[nx][ny], float y[ny]);
que calcule Y = X W, siendo x e y vectores fila y w una matriz.
Leer matriz
Implementar una función bool leer_matriz(size_t fs, size_t cs, float m[fs][cs])
que lea de stdin los valores que representan una matriz y los almacene en
m. La función debe devolver true en caso de poder leer la matriz, false
en caso contrario.
Esta función debe ser capaz de leer las matrices que imprime imprimir_matriz().
Aplicación 1
Se pide implementar un programa que lea de stdin dos matrices de pesos
\(W\) y \(V\) de dimensiones \(3\times2\) y que luego espere que el
usuario ingrese una sucesión indefinida de pares de valores \((i_0, i_1)\).
El programa debe computar la salida de la red neuronal definida por las matrices provistas para cada uno de los pares de valores que ingrese el usuario.
Por ejemplo, los siguientes valores definen una red entrenada de tal manera que \(o_0 = i_0 \lor i_1\) y \(o_1 = i_0 \land i_1\):
-4.92228079
5.38175964
-4.92212534
5.38191175
6.67276812
-3.39423680
-6.36431265
-14.04024220
13.64763451
8.00000095
-0.12261391
-1.46909201
Aplicación 2
Se pide implementar un programa que lea de stdin primero un entero n y
luego una cantidad n de
cuartetos \((i_0, i_1, o_0, o_1)\) y los use para entrenar una red neuronal
de con la geometría ya desarrollada.
El entrenamiento debe iniciarse con las matrices \(W\) y \(V\) inicializadas en valores aleatorios y realizar 10000 iteraciones con \(\eta = 0.5\) donde en cada iteración entrenará con cada uno de los valores de entrenamiento provistos.
Al terminar imprimirá por stdout las matrices de pesos \(W\) y \(V\).
Por ejemplo, la siguiente entrada se utilizó para entrenar los pesos ya dados:
4
0 0 0 0
0 1 1 0
1 0 1 0
1 1 1 1
Se presentan los valores en una única línea pero es totalmente equivalente a:
4
0
0
0
0
0
1
1
0
1
0
1
0
1
1
1
1
Entrega
Deberán entregarse los códigos fuentes de los dos programas desarrollados.
Ambos programas deben compilar correctamente con los flags:
-Wall -Werror -std=c99 -pedantic
y validar los ejemplos dados.
La entrega se realiza a través del sistema de entregas.
El ejercicio es de entrega individual.