Ejercicio obligatorio 2
Fecha de entrega: Lunes 7 de octubre
Nota
Nunca es buena idea empezar por un ejercicio integrador antes de tener practicados los temas que el trabajo integra.
Se sugiere antes de desarrollar este trabajo resolver, al menos, los siguientes ejercicios de la guía de Memoria dinámica:
Ejercicio 12 (combinar vectores).
Ejercicio 14.a (matriz identidad).
Ejercicio 16 con el 1.b y 1.c de la guía de estructuras (dirección y persona).
Introducción
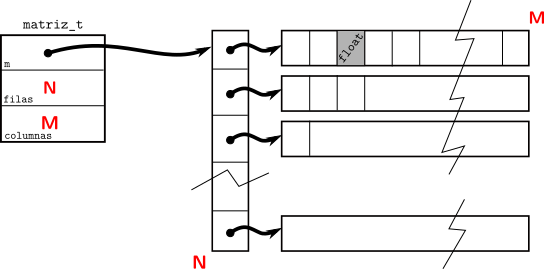
Queremos modelar una matriz, para ello definimos la estructura:
typedef struct {
float **m;
size_t filas, columnas;
} matriz_t;
que permite almacenar en memoria una matriz según el siguiente esquema:
Trabajo
Creación y destrucción
Se pide implementar la función auxiliar
matriz_t *_matriz_crear(size_t n, size_t m);
que genere la memoria necesaria para almacenar una matriz de n x m valores.
Los valores no deben ser inicializados. La función debe devolver la matriz
creada o NULL en caso de falla.
Se pide implementar la función void matriz_destruir(matriz_t *matriz);
que libere la memoria asociada a la matriz previamente creada.
Acceso a los datos
Se pide implementar una función
size_t matriz_filas(const matriz_t *matriz); que devuelve el número de
filas de la matriz.
Se pide implementar una función
size_t matriz_columnas(const matriz_t *matriz); que devuelve el número
de columnas de la matriz.
Se pide implementar una función
void matriz_dimensiones(const matriz_t *matriz, size_t *filas, size_t *columnas);
que devuelva la cantidad de filas y columnas de la matriz.
Se pide implementar una función
float matriz_obtener(const matriz_t *matriz, size_t fila, size_t columna);
que devuelva el valor almacenado en la posición fila, columna de la
matriz.
Generación de matrices
Implementar una función
matriz_t *matriz_leer(size_t n, size_t m); que cree una matriz de
n x m leyendo sus valores desde stdin. Los valores se leerán como n
líneas de entrada donde cada línea tendrá m valores separados por caracteres
blancos. La función debe retornar la matriz creada o NULL en caso de
falla.
Nota
Sugerencia: valerse de la función strtod() para poder realizar la lectura
de múltiples valores por línea.
Otra sugerencia: Utilizar un buffer de lectura de tamaño razonable, una sola línea puede ocupar muchos caracteres.
Extensión de matrices
Implementar una función bool matriz_extender(matriz_t *matriz); que
extienda en una columna a la matriz. Los elementos de la nueva columna deben
ser inicializados a 1. La función devuelve true si puede realizar la
operación.
Nota
Notar que esto cambia las dimensiones de la matriz, la misma debe reflejar
eso, por ejemplo si se llamara a matriz_columnas().
Algunas operaciones sueltas del EJ1
Implementar una función
matriz_t *matriz_multiplicar(const matriz_t *a, const matriz_t *b); que
devuelva \(A \times B\). En caso de falla o de no ser compatibles las
matrices recibidas debe devolver NULL.
Implementar una función
void matriz_aplicar(matriz_t *matriz); que le aplique a cada uno de los
elementos de la matriz la función sigmoidea.
Aplicación
Implementar un programa que lea de stdin tres números, de a uno por línea,
los cuales representan la cantidad de valores de entrada \(n_i\), la
cantidad de neuronas en la capa H \(n_h\) y la cantidad de valores de
salida \(n_o\). Luego se leerán de stdin la matriz \(W\) de tamaño
\(n_i + 1 \times n_h\) y la matriz \(V\) de tamaño
\(n_h + 1 \times n_o\). A partir de ese momento el programa leerá líneas
que contengan \(n_i\) valores cada una e imprimirá las \(n_o\)
respuestas correspondientes a aplicar la red neuronal definida por \(W\) y
\(V\).
Notar que el programa es casi idéntico a la aplicación 1 del EJ1 con la diferencia de que ahora se lee la cantidad de neuronas (que en el EJ1 eran 2, 2 y 2). Eso y el formato de lectura de las matrices que ahora está fijado.
Se proveen matrices de prueba.
Dos entradas, 2 neuronas H y tres salidas. Implementa or, and y xor lógicos:
2
2
3
6.56501722 7.78683090
6.56502056 7.78690529
-9.92721844 -3.81731486
3.38883948 12.47597790 -12.61389351
12.05436039 2.26307559 12.19962597
-5.83038235 -8.66410637 -5.81197023
Una entrada, 11 neuronas H y 4 salidas. Convierte los números del 1 al 10 en binario:
1
11
4
-5.30903816 7.05562210 6.21564150 6.97264194 6.91205835 -5.19426727 -4.47014189 4.65599775 3.93545413 3.58155107 3.64056873
29.06749725 -10.61930656 -21.03014374 -3.50132489 -3.52002954 38.90851593 11.63465214 -20.50225067 -25.48287964 -30.60029602 -35.00047302
-1.09161687 -2.17958021 -13.26340580 14.44618607
0.36545485 -2.89235520 12.05211067 -14.59816265
0.81871516 10.85333633 -14.98445129 -17.38402557
0.40498984 -3.21998858 -0.36098400 6.07753468
-0.01866573 -2.99007010 0.43762803 5.94211388
-12.18182278 11.69031906 17.91842461 15.41529465
-2.19953322 -9.84567356 -2.13680530 -18.18881798
1.58187580 1.64355898 0.33712316 14.09165287
3.21212530 -3.41997361 0.55070335 15.25783634
4.10961294 -5.31011677 5.06973982 17.36598206
5.69332218 -3.86532736 13.95511246 -18.34716797
-0.41404390 -5.60833073 -8.81380272 -17.24401283
Una entrada, 10 neuronas H y 1 salida. \(\sin(x)\) para \(0 \leq x \leq \pi\):
1
10
1
2.71614861 -1.40574467 4.68761539 5.74467134 10.74507427 0.30282176 -2.26366472 0.33558899 -5.11997700 0.41550291
-5.12603045 0.85895282 -7.40913248 -7.95125866 0.89139485 2.05528688 1.13089824 1.85756946 17.09574318 1.31795645
-5.69753170
-4.20246935
-7.05508184
8.87130547
8.72417450
-4.49026251
-4.55723953
-4.41047955
12.11481094
-4.32116795
-4.75244141
Tres entradas, 10 neuronas H y 8 salidas. Demultiplexa tres bits binarios:
3
10
8
5.51550627 -3.51880479 -4.17497206 4.22070169 6.12060881 -1.18278348 -4.63216162 4.55842161 -1.07078624 -1.24543619
-4.79343891 4.00000000 -3.64086080 3.27972960 5.00428200 5.67627478 4.38318682 -3.69111633 -1.35822213 3.25151992
-5.03890371 1.92246139 -2.55883217 3.81176400 -5.15021420 -0.72366685 -5.00612831 -0.50028527 7.01664734 -2.76531053
2.02090907 0.64594269 5.47741365 -4.95161104 -2.81993341 -1.70793676 2.46618867 1.73334968 -1.66325605 1.86461556
-5.42306423 4.13318586 2.88013625 3.53634501 -4.43884277 -4.97382593 -5.77240849 3.11494040
0.54221803 -0.26094633 -3.92973781 -6.64205408 -0.46005663 0.86798143 1.78058851 -1.86206388
-5.82063723 -8.24880314 -4.02215099 0.11427451 -2.83595467 0.63945079 4.46044064 1.58927715
0.85516322 2.81080627 4.14660931 -2.65783143 2.74227810 -4.77726746 -4.24465466 -6.74732018
6.25260544 0.90993214 -1.32604277 5.49917841 -6.72818708 2.63580370 -4.98032236 -7.92228127
2.16425943 2.35775399 -4.18162060 -4.09303427 3.46843743 2.42040920 -3.55587602 -2.12844801
-6.72060490 3.40531945 -3.65683985 -2.72658372 1.04992628 3.16677976 -3.50867558 5.27786732
-0.16477565 0.02259529 0.95917386 1.60429752 -7.18169880 -4.97218418 -0.77544403 0.41598016
1.83146882 -7.00004196 4.51100159 -6.02566099 3.18566704 -6.72487783 3.72872019 -3.59594154
-0.64314932 -0.43060106 -5.62132931 -1.49000144 0.72938317 0.17222236 -3.15672135 0.59198356
-3.54587221 -5.38373423 -3.05469370 -1.50358605 -2.16013718 -1.49478805 -0.22054017 -1.60520017
Nota
NO se pide en este enunciado. Pero si te interesara entrenar tus propias redes, las ecuaciones para el backpropagation son las mismas que las del EJ1. Tené en cuenta que cambian las dimensiones nomás:
Los índices \(w_{ij}\) tienen \(i = [0 \mathrel{{.}\,{.}} n_i + 1)\), \(j = [0 \mathrel{{.}\,{.}} n_h)\).
Los índices \(v_{ij}\) tienen \(i = [0 \mathrel{{.}\,{.}} n_h + 1)\), \(j = [0 \mathrel{{.}\,{.}} n_o)\).
En el cálculo de \(\frac{\partial L}{\partial w_{ij}}\) la sumatoria tiene \(k = [0 \mathrel{{.}\,{.}} n_o)\).
Se insiste en que no es parte de este trabajo.
Entrega
Deberá entregarse el código fuente del programa desarrollado.
El programa debe:
Compilar correctamente con los flags:
-Wall -Werror -std=c99 -pedantic
pasar Valgrind correctamente,
La entrega se realiza a través del sistema de entregas.
El ejercicio es de entrega individual.