Trabajo Práctico 1

Fecha de entrega: Lunes 2 de diciembre

Introducción

Objetivo

El objetivo del presente trabajo práctico es implementar una biblioteca de redes neuronales multicapa y luego utilizar esa biblioteca para implementar un sistema de reconocimiento de textos (OCR).

El trabajo consiste en la resolución de un problema mediante el diseño y uso de TDAs y en la reutilización de algunos de los tipos, funciones y conceptos desarrollados a lo largo del curso en trabajos anteriores.

Alcances

Mediante el presente TP se busca que el estudiante adquiera y aplique conocimientos sobre los siguientes temas:

Encapsulamiento en TDAs,
Contenedores y tablas de búsqueda,
Punteros a funciones,
Archivos,
Modularización,
Técnicas de abstracción,

además de los temas ya evaluados en trabajos anteriores.

Nota

Este trabajo es un trabajo integrador de final de cursada. En el mismo se van a aplicar todos los temas aprendidos y además se va a evaluar el diseño de la aplicación.

Es imprescindible entender los temas de TDA y modularización antes de empezar con el trabajo.

Es imprescindible diseñar el trabajo como etapa previa a la implementación.

Cualquier abordaje que pretenda empezar a codificar sin haber ordenado el trabajo primero está condenado a fracasar contra la complejidad del problema.

Un repaso por las redes neuronales multicapas

En los trabajos anteriores presentamos el modelo de red neuronal donde hay capas de neuronas. La primera capa es la capa de entrada, con tantas neuronas como parámetros de entrada (más una adicional para el bias). La última capa es la capa de salida, con tantas neuronas como parámetros de salida.

En el modelo que presentamos en los ejercicios anteriores entre la entrada y la salida había una capa oculta, que llamamos \(H\), con una determinada cantidad de neuronas (más el bias).

Cada una de las capas se vincula por la siguiente por una matriz de pesos, que conecta todas las neuronas de la capa anterior con todas las de la capa siguiente.

En una red neuronal multicapa no tenemos por qué limitarnos a una capa de neuronas ocultas si no que podemos tener tantas como queramos.

Como ya sabemos, la propagación de la información entre cada capa consiste en la multiplicación de las neuronas de entrada (más el bias) por la matriz de pesos y luego pasar cada uno de los resultados por la función de activación. En los ejercicios anteriores utilizamos la función sigmoidea como función de activación pero podemos utilizar otras funciones.

Para el entrenamiento de la red podemos generalizar sencillamente las fórmulas de backpropagation para funcionar con otras funciones de activación y para tener cualquier número de capas.

Funciones de activación

Como ya sabemos la función de activación que aplicamos cuando computamos la salida de una red, tenemos que evaluarla según su derivada cuando aplicamos el algoritmo de backpropagation.

Vamos a dar una serie de funciones de activación y sus respectivas derivadas (en función de su salida):

Sigmoidea:
Ya conocemos a la función sigmoidea \(f(x) = \frac1{1 + \exp(-x)}\) y también conocemos su derivada \(f(x)' = f(x) (1 - f(x))\).

Identidad:
La función identidad es sencillamente \(f(x) = x\) con \(f(x)' = 1\).

ReLU:
La función Rectified Linear Unit (ReLU) \(f(x) = \max{0, x}\) o, dicho de otro modo, \(0 \mbox{ si } x < 0,\quad x \mbox{ si } x \geq 0\) y su derivada (en función de \(f(x)\)) es sencillamente \(f(x)' = 0 \mbox{ si } f(x) = 0,\quad 1 \mbox{ si } f(x) > 0\).

Tangente hiperbólica:
Podemos dar la expresión de la función tangente hiperbólica, pero la misma ya viene implementada en la biblioteca matemática tanhf(). Su derivada es \(f(x)' = 1 - f(x)^2\).

Backpropagation

En el EJ1 desarrollamos una fórmula de backpropagation para actualizar cada una de las dos matrices de pesos que teníamos. Sin importar la cantidad de capas, la actualización de la última capa debería ser idéntica a esa. Recordemos, habíamos llegado a esta expresión:

\[\frac{\partial L}{\partial v_{ij}} = \left[ o_j - \hat o_j \right] \left[ o_j (1 - o_j) \right] \left[ h_i \right]\]

En esa fórmula el término \(\left[ o_j (1 - o_j) \right]\) no es otra cosa que la derivada de la función sigmoidea en función de la salida. Genéricamente tendríamos:

\[\frac{\partial L}{\partial v_{ij}} = h_i \left[ \left( o_j - \hat o_j \right) f(o_j)' \right]\]

Es decir, sólo tres términos: Al comienzo la entrada desde la capa anterior eso multiplicando a la diferencia entre el valor calculado y el valor deseado multiplicado por la derivada de la activación evaluada en el valor calculado.

Esta fórmula funciona para cualquiera de las funciones de activación que vimos. Y cabe decir que cada capa puede tener una función de activación diferente.

Si recordamos del EJ1, la fórmula para la última capa era fácil, pero la fórmula para la primera capa era mucho más complicada... bueno, en realidad no. Era complicado el formuleo que dimos para la primera capa, porque no teníamos las herramientas necesarias para simplicar esa fórmula todavía.

El algoritmo de backpropagation básicamente lo que mira es cómo el peso que queremos corregir incide en la salida. ¿Por qué es tan fácil para la última capa? Básicamente porque en la última capa cada peso afecta a una única salida. En nuestra fórmula anterior, el peso \(v_{ij}\) afecta únicamente a la salida \(o_j\).

En el EJ1 (mirar el gráfico de ahí) para los pesos de \(w_{ij}\) es más complicado porque afectan a la neurona \(h_j\) y a su vez esta neurona está unida a cada una de las salidas \(o_k\). O sea, hay múltiples caminos para llegar desde \(h_j\) a la salida. De ahí viene la sumatoria que operamos (que era hasta 2, porque en ese ejercicio había sólo dos salidas, si hubiéramos implementado lo mismo en el EJ2 hubiéramos iterado por cada salida).

Dicho todo esto, recordemos las fórmulas del EJ1 para la primera capa:

\[\frac{\partial L}{\partial w_{ij}} = \sum_{k=0}^{n_o} \left[ o_k - \hat o_k \right] \left[ o_k (1 - o_k) \right] \left[ v_{jk} \right] \left[ h_j (1 - h_j)\right] \left[ i_i \right].\]

Limpiemos un poco esto, por empezar, saquemos los términos de la sigmoidea, y por seguir separemos los términos que dependen del \(k\) de la sumatoria de los que no:

\[\frac{\partial L}{\partial w_{ij}} = i_i \left[ f(h_j)' \sum_{k=0}^{n_o} \left( o_k - \hat o_k \right) f(o_k)' v_{jk} \right].\]

El uso de corchetes en las dos ecuaciones que reordenamos es arbitrario pero están puestos para destacar cosas. En ambos casos el primer término es la entrada desde la capa anterior. De esta nueva expresión miremos dentro de la sumatoria el término \((o_k - \hat o_k) f(o_k)'\), ¿suena conocido? Bueno ese es el aporte de la capa de salida a la neurona \(w_{ij}\) y hay una sumatoria porque hay tantos aportes como neuronas haya en esa capa. ¿Cómo sería esto si en vez de dos capas hubiera más capas? En ese caso empezaríamos a tener cada vez más caminos posibles para llegar desde la entrada a la salida, es decir sumatorias metidas adentro de sumatorias adentro de sumatorias... ¿pero no dijimos que íbamos a resolverlo más sencillo? Sí, claro.

Empecemos de nuevo.

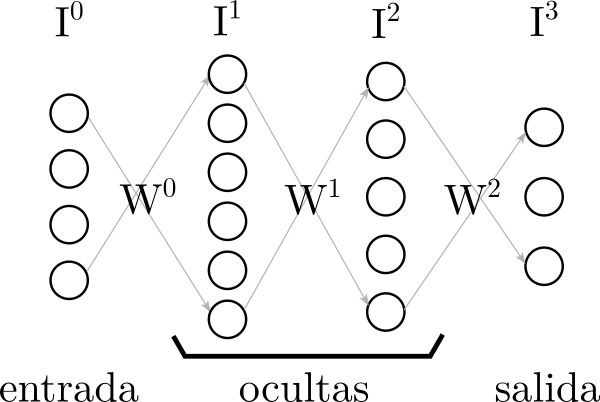
Tenemos una red neuronal con \(N\) capas. La primera capa es la de entrada, la última es la de salida, en el medio están las ocultas. En el EJ1 y EJ2 implementamos una red de 3 capas. En una red de \(N\) capas hay \(N - 1\) matrices \(W^n\) de pesos que vinculan las \(N\) capas entre sí. Llamemos a la capa de entrada \(I^0\) y llamemos \(I^n\) a las siguientes capas de neronas. La capa de salida \(O = I^n\). (Y estamos llamando \(I^1\) a la que antes llamábamos \(H\).)

Entonces, tenemos \(N\) capas \(I^n\) y \(N - 1\) matrices \(W^n\).

Definamos para la última matriz, la \(N - 1\) la siguiente fórmula:

\[\varepsilon(n, j) = (o_j - \hat o_j) f^n(o_j)', \quad \mbox{ si } n = N - 1.\]

Ahora definamos para las demás matrices la siguiente fórmula:

\[\varepsilon(n, j) = f^n(I^{n+1}_j)' \sum_{\forall k} w^{n+1}_{jk} \varepsilon(n+1, k), \quad \mbox{ si } n \neq N - 1.\]

Es decir, para la capa \(n\) tendremos la derivada de la salida en ese punto, donde la salida no es otra cosa que el valor ya computado en la capa \(I\) siguiente(*), la capa \(n + 1\). Luego una sumatoria para todas las neuronas de la siguiente capa con el peso que vincula a cada una de ellas con esta neurona y luego el aporte a la salida de ella... que no es otra cosa que una llamada recursiva. Esa llamada recursiva es la que va a propagar hasta el final de la red los múltiples caminos para llegar a nuestra neurona.

(*: Si bien estamos utilizando la convención de nombrar matrices y vectores en mayúsculas y a sus elementos en minúscula, utilizamos mayúscula para \(I\) en esta fórmula para que no se confunda después con los índices.)

Teniendo esta función definida entonces podemos calcular los términos del backpropagation como:

\[\frac{\partial L}{\partial w^n_{ij}} = I^n_i \varepsilon(n, j).\]

Y, al igual que en el EJ1:

\[{W^n}' = W^n - \eta \frac{\partial L}{\partial W^n}.\]

Tipografías

Se tienen archivos BMP con tipografías monoespaciadas. Que sean monoespaciadas significa que todos los caracteres ocupan exactamente el mismo ancho.

Por ejemplo, podemos tener el siguiente archivo abcd.bmp:

El mismo viene, además acompañado del siguiente archivo abcd.txt:

La primera línea del archivo de texto indica la cantidad y las dimensiones de cada carácter. En este caso, son 4 caracteres de 10 píxeles de ancho por 20 de alto. Luego viene un número por cada uno de los caracteres contenidos en el texto que indica qué carácter es. Finalmente viene una cadena con la traducción de los números anteriores en cómo se representa ese carácter. (¿Por qué decimos cadena?, porque por ejemplo el carácter "Ñ" se representa en múltiples bytes en Unicode)

La imagen BMP tiene que ser de 40x20, porque contiene 4 caracteres de 10x20. Los caracteres en la imagen siempre estarán en una única fila uno detrás del otro.

Notar que la misma imagen BMP podría ir acompañada del texto:

Los caracteres de entrenamiento son los mismos, pero sólo se clasifican en 2 clases, A y a serán el carácter 0 -> A, y Ñ y ñ serán el 1 -> Ñ.

Textos

Además habrá imágenes con textos, que se corresponderán a alguna tipografía ya dada, por ejemplo el siguiente texto:

es una imagen de 500x160 píxeles. Como cada carácter tiene 10x20 sabemos que cada línea tiene 50 caracteres y que consta de 8 líneas.

Imágenes a redes neuronales

Si se quiere implementar una red neuronal que aprenda una tipografía cada uno de los pixeles de un carácter será una entrada, mientras que cada uno de los carácteres será una salida.

Para nuestra tipografía de ejemplo, como cada carácter tiene 10x20 habrá entonces 200 entradas. Y como hay 4 caracteres diferentes habrá 4 salidas. (En la versión alternativa del TXT habría 2 salidas porque si bien hay 4 muestras representan sólo 2 caracteres diferentes.)

Como se trata de identificar una letra la salida será una clasificación. Por ejemplo, para el primer carácter, la letra A, la salida deberá ser \((1, 0, 0, 0)\). Cuando ejecutemos la red neuronal ya entrenada contra un texto desconocido la neurona que esté más activada a la salida será la que indique qué carácter se reconoció.

El trabajo

TDAs

Además de los TDA matriz_t e imagen_t debe desarrollarse al menos un TDA para el manejo de la red neuronal.

`matriz_t`

A las primitivas que ya se tienen del TDA matriz_t deben agregarse al menos las siguientes:

Constructor random:
Un constructor para construir una matriz de determinado tamaño inicializada de forma aleatoria.

A diferencia del EJ1 inicializaremos en este caso la matriz con números aleatorios entre \([-x; x]\) con \(x = \sqrt{\frac6{f + c}}\), siendo \(f\) y \(c\) la cantidad de filas y columnas de la matriz respectivamente.

Aplicar:
La primitiva matriz_aplicar() ahora tendrá la firma void matriz_aplicar(matriz_t *m, float (*funcion)(float); y recibirá la función que debe aplicar.

Escritura:
Una primitiva que dado un FILE * pueda volcar la matriz en un archivo binario.

Lectura:
Un constructor que dado un FILE * pueda leer una matriz de él según el formato binario con el cual se escribió.

Red neuronal

Se debe implementar un TDA que permita modelar una red neuronal multicapa y que permita entrenar y evaluar la red neuronal.

El TDA se comunicará hacia el exterior con objetos de tipo matriz_t, es decir una entrada será una matriz, la salida esperada será una matriz, y la respuesta al aplicar la red será una matriz.

La representación interna de la red, así como las matrices de pesos serán internas del TDA.

La red neuronal tiene que poder ser construída indicándole la cantidad de capas, la cantidad de neuronas en cada capa y las funciones de activación de cada capa. Sin ser esto una especificación un ejemplo podrían ser constructor(4, {3, 10, 20, 5}, {RELU, RELU, SIGMOIDEA}) los parámetros para construir una red de 4 capas, con 3 entradas, 5 salidas y 10 y 20 neuronas en las capas ocultas activadas por las funciones que se indican.

La red neuronal tiene que tener una primitiva para realizar un guardado a disco binario y un constructor para reconstruirla desde un archivo. (De más está decir que para escribir en disco las matrices se delegará esa funcionalidad en las primitivas de dicho TDA.)

Tiene que tener una primitiva que dado un vector (matriz de 1 x entradas) devuelva un vector con la respuesta de la red para ese vector.

Además tiene que tener una primitiva que dado un vector de entrada y uno con la salida deseada, además de un \(\eta\), realice una única iteración de entrenamiento de la red. La función debe devolver el error cuadrático ya presentado en el EJ1:

\[L = \frac12 \sum_{i = 0}^{N_o} \left(\hat o_i - o_i \right)^2\]

Es decir, Bárbara podría utilizar la red neuronal entrenándola de forma incremental según el siguiente pseudocódigo:

Para ciclos = 1 .. 1000:
    l = 0
    Para cada muestra:
        l += entrenar(entrada[muestra], salida[muestra], eta)
    Imprimir("Ciclo: %d, Error: %f", ciclo, l)

Las aplicaciones

Ya se dijo todo lo previo que había por decir.

El problema que se plantea en este trabajo deberá ser resuelto con las herramientas ya adquiridas, extendiendo de forma consistente los TDAs ya planteados de ser necesario y diseñando los TDAs nuevos que hagan falta. Se evaluará además el correcto uso de los TDAs respetando la abstracción y el "modelo" de Alan-Bárbara.

A esta altura del cuatrimestre es una obviedad decirlo pero: Todo lo que pueda ser iterativo o implementarse de forma indexada, debe ser hecho de esa manera. Todo lo que amerite tablas de búsqueda debe utilizarlas.

Entrenamiento de red neuronal

Para entrenar una red neuronal necesitamos:

Una tipografía (que consiste en dos archivos, el BMP y el TXT)

Una cantidad de iteraciones que se van a realizar

Un grado de aprendizaje \(\eta\)

Y además una de estas dos cosas:

O un archivo binario que represente un estado anterior de la red que ya está entrenada en parte y queremos seguir entrenando

O la información de cuántas capas, cuántas neuronas y qué funciones de activación queremos para construir una nueva red desde cero

(Siendo que una red va a entrenar una determinada tipografía, es una buena decisión de diseño que el entrenamiento sea un .bin del mismo nombre que el BMP y el TXT, incluso si existe el bin puede asumirse que ya hay un entrenamiento previo.)

Implementar una aplicación que se le pasen por CLA la tipografía, iteraciones y grado de aprendizaje. Se deja a criterio del alumno cómo informar la cantidad de capas, etc. para una red nueva. Pero así como se deja a criterio tiene que estar documentado y se debe proveer un ejemplo. El docente que corrija no puede estar adivinando cómo se utiliza la aplicación.

La aplicación debe correr esa cantidad de iteraciones cada uno de los caracteres de la tipografía e ir informando del error para cada una de las iteraciones. Al finalizar debe escribir en disco la red neuronal entrenada.

Programa de reconocimiento de caracteres

Implementar una aplicación que se la invoque pasándole una tipografía con su entrenamiento y una imagen por CLA e imprima el texto que contiene la imagen. Por ejemplo:

$ ./20242_tp1_ocr tipografia quijote.bmp
En un lugar de la Mancha, de cuyo nombre no quiero
acordarme, no ha mucho tiempo que vivía un hidalgo
de los de lanza en astillero, adarga antigua,
rocín flaco y galgo corredor. Una olla de algo más
vaca que carnero, salpicón las más noches, duelos
y quebrantos los sábados, lantejas los viernes,
algún palomino de añadidura los domingos,
consumían las tres partes de su hacienda.
$

Requisitos

Los únicos requisitos son que el programa resuelva correctamente la funcionalidad pedida y que lo haga utilizando TDAs con un diseño planificado a conciencia. Si hacés eso nada puede salir mal.

Entregables

Deberá entregarse:

El código fuente del trabajo debidamente documentado.

El archivo Makefile para compilar el proyecto.